|
Graphisches Lösen
Das gegebene Problem ist dergestalt, dass wir es graphisch in der Ebene
lösen können.
Dazu werden zuerst kalkülmäßig die Zielfunktion und die Nebenbedingungen
formuliert. Die Nebenbedingungen sind Ungleichungen. Die graphische Veranschaulichung
der Nebenbedingungen ergibt Schnitte von Halbebenen, deren Ergebnis im vorliegenden
Fall ein begrenztes Gebiet ist, der sogenannte zulässige Bereich
(Abbildung 2). Der zulässige Bereich enthält alle
Punkte der Ebene, deren Koordinaten die Nebenbedingungen erfüllen.
Als Repräsentation der Zielfunktion wird eine
Optimierungsgerade eingeführt. Diese wird so lange parallel in
Optimierungsrichtung verschoben (der Absolutwert der verschobenen Gerade muss kleiner
werden, weil die Zielfunktion minimiert werden soll), bis die Optimierungsgerade eben
noch den zulässigen Bereich tangiert. Dieser "letzte" Berührungspunkt der
Optimierungsgerade mit dem zulässigen Bereich ist der optimale Punkt, seine
Koordinaten sind die gesuchten Werte und .
Lineare Funktionen besitzen die Eigenschaft der Konvexität. Daher können wir
den Sachverhalt nutzen, dass der "letzte" gemeinsame Punkt der
Optimierungsgerade mit dem zulässigen Bereich ein Eckpunkt ist.
Es reicht demzufolge aus, die Gerade in alle Eckpunkte parallel zu verschieben und dabei
den Absolutwert der Gerade, die Ordinate des Schnittpunktes mit der
Ordinatenachse, zu betrachten (Abbildung 2).
Es bezeichne die Anzahl der einzukaufenden Platten des Typs ,
es bezeichne die Anzahl der einzukaufenden Platten des Typs .
Modellieren wir die im Aufgabentext angegebenen Aussagen in Formeln,
entsteht das folgende Optimierungsproblem. Die zugehörige Zielfunktion
lautet:
|
|
(1) |
Als Nebenbedingungen ergeben sich die Ungleichungen (die Bezeichnung entspricht den Bedingungen, die
an die einzelnen Plattentypen gestellt werden):
| (A) |
|
|
|
≥ |
10 |
|
| (B) |
x |
+ |
2y |
≥ |
12 |
|
| (C) |
x |
+ |
y |
≥ |
8 |
|
| (D) |
|
|
2y |
≥ |
4 |
|
| (D') |
|
|
2y |
≤ |
16 |
|
| (E) |
x |
|
|
≤ |
5 |
|
| (N) |
|
|
x, y |
≥ |
0 |
(x, y ganzzahlig) |
|
(2)
|
Zur besseren graphischen Darstellbarkeit wird (1) und (2)
umgeformt, es entsteht als Zielfunktion:
|
y=-32x+G*
|
, wobei gilt
|
G*=G200=Min!
|
(3) |
Als Nebenbedingungen entstehen die folgenden Ungleichungen für ganze x und y:
| (A) |
y |
≥ |
-2x |
+ |
10 |
|
| (B) |
y |
≥ |
-12x |
+ |
6 |
|
| (C) |
y |
≥ |
-x |
+ |
8 |
|
| (D) |
y |
≥ |
|
|
2 |
|
| (D') |
y |
≤ |
|
|
8 |
|
| (E) |
0 |
≤ |
-x |
+ |
5 |
|
| (N) |
x, y |
≥ |
|
|
0 |
. |
|
(4)
|
Durch den Eintrag in ein Koordinatensystem in der Ebene gelangen wir nun zum
zulässigen Bereich durch den Schnitt der Halbebenen, die in (4) definiert
sind (Abbildung 2).
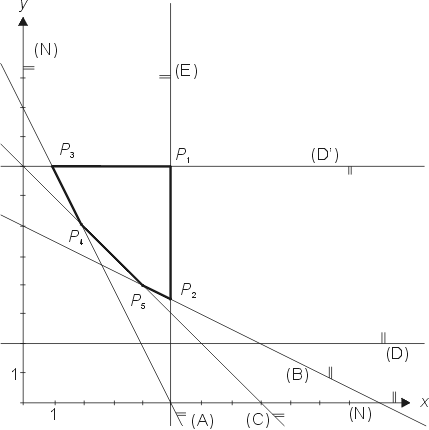
Abbildung 2: Ermittlung des zulässigen Bereichs.
Als Eckpunkte des zulässigen Bereiches ergeben sich die Koordinatentupel
P158,
P253,5,
P318,
P426 und
P544.
Da an eine Lösung des Optimierungsproblems die Forderung der Ganzzahligkeit gestellt wird,
werden die Eckpunkte mit nichtganzzahligen Koordinaten (im Beispiel P2)
nicht weiter berücksichtigt.
Zeichnen wir im Koordinatensystem eine Schar von Parallelen, die
verschiedenen G* entsprechen, so dass jeweils die (ganzzahligen!)
Eckpunkte des zulässigen Bereichs auf den Geraden liegen (Abbildung 3),
ergeben sich die Absolutwerte der Geraden mit
G1*=15,5;
G3*=9,5;
G4*=9 und
G5*=10;
Betrachten wir aufgrund der Minimierung von
G* die
Optimierungsrichtung in Richtung der negativen y-Achse, erkennen
wir, dass G* den Minimalwert annimmt und gerade noch den zulässigen
Bereich in dem Eckpunkt
xy=26
tangiert, wenn
G*=G4*=9 gilt.
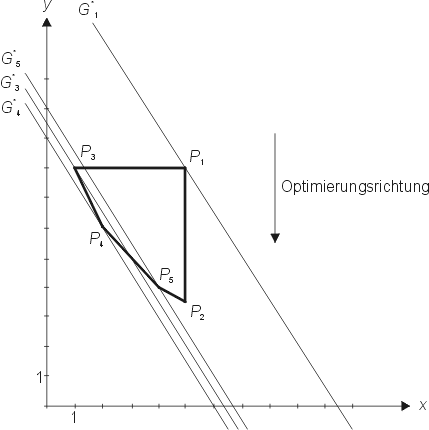
Abbildung 3: Suchen der Optimalstelle durch Minimierung.
Also besitzt das lineare Optimierungsproblem folgende Lösung:
Es sind genau 2 Platten des Typs I und 6 Platten des Typs II einzukaufen,
der Einkaufswert beträgt
G=1800 Euro.
Graphische Lösungen bieten sich bei zweidimensionalen Problemen aber auch an,
wenn nur die Nebenbedingungen linear sind und die Zielfunktion
beispielsweise quadratisch auftritt.
Nicht unerwähnt bleiben soll das graphische Lösen dreidimensionaler linearer
Optimierungsprobleme. Einfache räumliche Aufgaben unterstreichen
die Komplexität der mathematischen Optimierung, schulen das
Vorstellungsvermögen und sind in komplizierterer Form ein hervorragender
Einstieg in vieldimensionale Problematiken, hinarbeitend auf die
Simplexmethode.
|





