|
Die Dreiteilung des Winkels
Während die Zweiteilung eines gegebenen Winkels auf konstruktivem Wege mit Zirkel und Lineal
sehr einfach bewältigt werden kann, stellt sich das Problem der Dreiteilung - abgesehen von ausgezeichneten Winkeln - als
unlösbar für die elementaren Konstruktionsschritte mit Zirkel und Lineal heraus.
Aufgabe:
Teile einen beliebigen Winkel durch endlich viele
Konstruktionsschritte in drei gleich große Winkel.
|
|
Die algebraische Formulierung des Konstruktionsproblems führt zu einer Gleichung, deren strukturelle Analyse weitere Auskunft über
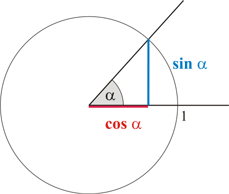
die Konstruierbarkeit der Dreiteilung geben wird. Dabei wird auf die Eineindeutigkeit der Zuordnung eines Winkels zu seinem Kosinus
zurückgegriffen: Ist die Größe eines Winkels bekannt, lässt sich am Einheitskreis eindeutig die Länge des Kosinus des Winkels
konstruieren und vice versa (Abbildung).
|
|
Abbildung: Sinus und Kosinus eines Winkels am Einheitskreis.
|
Diese eineindeutige Zuordnung ermöglicht es, von der Bestimmung eines Winkels zur Bestimmung des Kosinus des Winkels überzugehen.
Im Folgenden bezeichne den Winkel, der gedrittelt werden soll. Somit ist
derjenige Winkel, dessen Größe bei gegebenen zu bestimmen ist.
Ausgehend von den aus der Trigonometrie bekannten Zusammenhängen
| (1) |
|
mit dem Spezialfall |
(1') |
|
| (2) |
|
mit dem Spezialfall |
(2') |
|
| (3) |
|
folgt bei gegebenem Winkel :
| |
|
|
|
| |
|
|
nach (2) |
| |
|
|
nach (2') und (1') |
| |
|
|
nach Ausmultiplizieren |
| |
|
|
nach Zusammenfassen |
| |
|
|
nach (3) |
| |
|
|
nach Zusammenfassen |
| |
|
|
nach Umsortieren. |
Mit der gegebenen Größe ist auch die Größe bekannt.
Somit liegt eine kubische Gleichung vor, die sogenannte Dreiteilungsgleichung, deren Auflösung zu den Werten
führt. Aus den Lösungen für
können Werte des Drittelwinkels bestimmt werden.
Die soeben angeführte und eine weitere Variante der Herleitung einer Dreiteilungsgleichung (über Ähnlichkeitsbetrachtungen am Einheitskreis)
finden sich bei Walter Breidenbach:
Die Dreiteilung des Winkels, S. 11 f.
Eine Herleitung über Lösbarkeitsbetrachtungen einer Gleichung dritten Grades der Form
ist nachlesbar bei Felix Klein: Vorträge über ausgewählte Fragen der Elementargeometrie, S. 10 ff.
Die algebraische Betrachtung der Lösbarkeit der Dreiteilungsgleichung führt dann direkt zur Frage der Konstruierbarkeit der Lösungen,
mithin zur Frage nach der Möglichkeit oder Unmöglichkeit der konstruktiven Dreiteilung des gegebenen Winkels.
Von großem Einfluss für die Konstruierbarkeit des Drittelwinkels ist die Größe des Ausgangswinkels, da diese als Absolutglied in der
Dreiteilungsgleichung maßgeblich über die Art der Lösungen entscheidet. Besitzt die Dreiteilungsgleichung für einen gegebenen Ausgangswinkel
wenigstens
eine reelle Lösung, die durch rationalen Operationen (Addition, Subtraktion, Multiplikation und Division) oder durch das Ziehen
von Quadratwurzeln herstellbar ist, so ist diese Lösung konstruierbar.
Breidenbach hat als Kriterium formuliert, dass nur bei der Existenz einer rationalen Lösung der
Dreiteilungsgleichung die Dreiteilung des Winkels konstruktiv erfolgen kann. Liegt eine solche Lösung nicht vor,
ist das Problem der Dreiteilung konstruktiv mit Zirkel und Lineal unlösbar. (siehe Walter Breidenbach:
Die Dreiteilung des Winkels, S. 17 ff.)
|





