Die Epizykloide

Die relative Bewegung von Kreisen zueinander ist bereits seit der Antike mit der Theorie der Epizyklen bekannt, die vermutlich auf Apollonius von Perge (262 - ca. 190 v.u.Z.) zurückgeht [van der Waerden, S. 395 ff.]. Im Jahr 1525 konstruierte Albrecht Dürer seine Spinnenlinie [Dürer, Abbildung 40] als Bahnkurve eines festen Punktes auf der Peripherie eines Kreises, der entlang eines Leitkreises abrollt. Dies ist die erste bekannte Darstellung einer Epizykloide. Die erste methodische Behandlung der Epizykloiden wurde 1679 von Philippe de La Hire (1640-1718) veröffentlicht, allerdings unter direktem Bezug auf die Urheberschaft von Girard Desargue (1591-1661), der epizykloide Eigenschaften bei der Konstruktion möglichst reibungsfreier Zahnradkombinationen untersuchte. ([Loria 1911, S. 93 f.] und [Cantor 1892, S. 621])

Geometrische Konstruktion

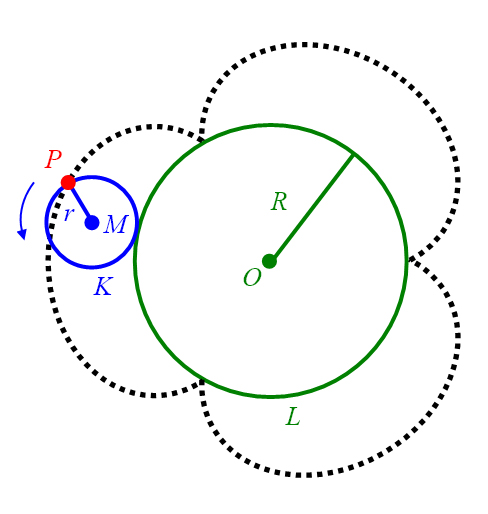
In einer Ebene rollt ein Kreis $K$ mit dem Mittelpunkt $M$ ohne zu gleiten auf der Kreislinie eines Leitkreises $L$ mit dem Mittelpunkt $O$ ab. Der Rollkreis $K$ befindet sich dabei außerhalb der Kreisfläche von $L$. Der Radius des Rollkreises $K$ sei als $r$ gegeben, der Radius des Leitkreises sei $R$. Ein fester Punkt $P$ der Kreislinie des Rollkreises $K$ beschreibt beim Abrollen eine Bahnkurve, die als gewöhnliche Epizykloide bezeichnet wird (Abbildung 26, links).

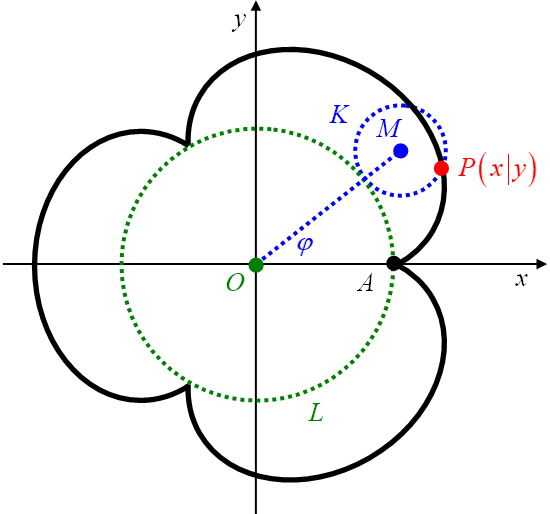
Abbildung 26: Geometrische Konstruktion einer Epizykloide (links) und Lage der Epizykloide im Koordinatensystem (rechts).

Kurvengleichung und geometrische Besonderheiten

In die Ebene wird ein kartesisches Koordinatensystem so eingebracht, dass der Koordinatenursprung im Mittelpunkt $O$ des Leitkreises $L$ liegt und die $x$-Achse einen Anfangspunkt $A$ der Bahnkurve enthält. Ein Anfangspunkt ist dadurch gekennzeichnet, dass der feste Punkt $P$ gleichzeitig Berührungspunkt bzw. Auflagepunkt von $K$ auf $L$ in der Rollbewegung ist (Abbildung 26, rechts).

Mit Hilfe des Winkels $\phi =\angle MOA$ lässt sich die Lage des Rollkreises eindeutig beschreiben. In Abhängigkeit von $\phi$ entstehen für die Koordinaten der Kurvenpunkte der gewöhnlichen Epizykloide parametrische Darstellungen:

	Gewöhliche Epiykloide:		${\displaystyle x=\left(r+R\right)\cdot cos\phi -r\cdot cos\left(\frac{r+R}{r}\cdot \phi \right)}$
			${\displaystyle y=\left(r+R\right)\cdot sin\phi -r\cdot sin\left(\frac{r+R}{r}\cdot \phi \right)}$
			mit   ${\displaystyle -\mathrm{\infty }<\phi <\mathrm{\infty }}$

Das Verhältnis ${\displaystyle m=\frac{R}{r}}$ der beiden Kreisradien des Leitkreises und des Rollkreises bestimmt die Gestalt der epizykloidalen Bahnkurve hinsichtlich der Anzahl der Kurvenbögen und ihrer Geschlossenheit.

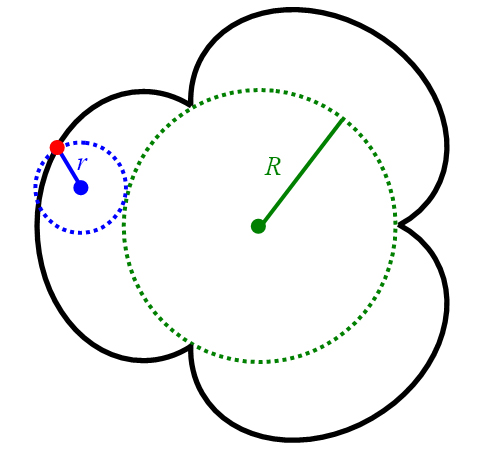
Ist $m$ positiv ganzzahlig, so besteht die Kurve aus $m$ Bögen und die Kurve ist geschlossen, d.h. sie endet im Anfangspunkt (Abbildung 27, links). Ein Sonderfall liegt für $R=r$ vor: die gewöhnliche Epizykloide wird zu einer Kardiode.
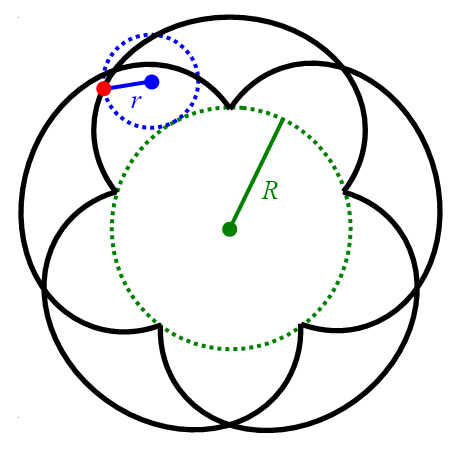
Ist $m$ eine echt rationale Zahl ${\displaystyle \frac{p}{q}}$, so besteht die Kurve aus $p$ Bögen und die Kurve ist nach $q$ Umläufen des Rollkreises geschlossen (Abbildung 27, rechts).
Ist $m$ eine irrationale Zahl, besteht die Kurve aus unendlich vielen Kurvenbögen und ist nicht geschlossen.

Abbildung 27: Gewöhnliche Epizykloiden im Verhältnis der Radien $R:r=3:1$ (links) und $R:r=5:2$ (rechts).

Die periodisch auftretenden Anfangs- und Endpunkte der Kurvenbögen der gewöhnlichen Epizykloidenkurve stellen Singularitäten dar, da die Kurve dort in Spitzen ausläuft.

Verkürzte und verlängerte Epizykloide

Mit einer verallgemeinerten Lage des festen Punktes $P$ in Bezug auf den Rollkreis entstehen beim Abrollen von $K$ auf einem Leitkreis $L$ verlängerte oder verkürzte Epizykloiden.

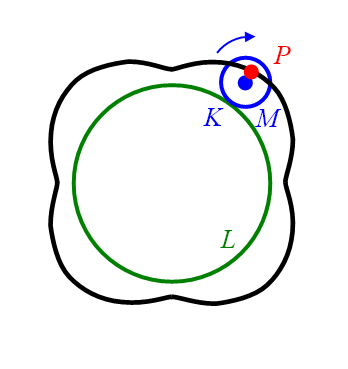
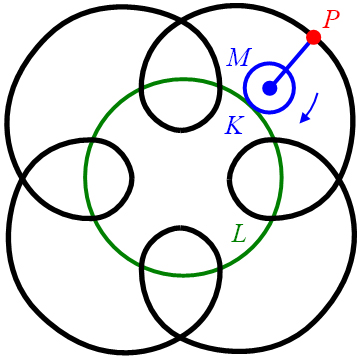
Bezeichne $a$ den Abstand ${\displaystyle \left|\stackrel{\_}{MP}\right|}$. Liegt $P$ innerhalb der Kreisfläche des Rollkreises, gilt also $a<r$, so entsteht als Bahnkurve des Punktes $P$ eine verkürzte Epizykloide (Abbildung 28, links). Liegt $P$ außerhalb der Kreisfläche von $K$, gilt also $a>r$, so entsteht eine verlängerte Epizykloide (Abbildung 28, rechts).

Abbildung 28: Verkürzte Epizykloide (links) und verlängerte Epizykloide (rechts) jeweils mit Leitkreis $L$ und abrollendem Kreis $K$.

Die Koordinaten der Kurvenpunkte der verkürzten und verlängerten Epizykloide lassen sich analog zur gewöhnlichen Epizykloide in Parameterform ausdrücken:

	Verkürzte bzw. verlängerte Epizykloide:		${\displaystyle x=\left(r+R\right)\cdot cos\phi -a\cdot cos\left(\frac{r+R}{r}\cdot \phi \right)}$
			${\displaystyle y=\left(r+R\right)\cdot sin\phi -a\cdot sin\left(\frac{r+R}{r}\cdot \phi \right)}$
			mit   ${\displaystyle -\mathrm{\infty }<\phi <\mathrm{\infty }}$   und   ${\displaystyle \frac{a}{r}<1}$   bzw.   ${\displaystyle \frac{a}{r}>1}$

Die verkürzte Epizykloide weist keine singulären Punkte auf. Die verlängerte Epizykloide besitzt in periodisch wiederkehrender Folge Singularitäten in Form von Doppelpunkten.