Die Zykloide

Bereits 1501 betrachtete Charles de Bouvelles (1471-1553) die Bahnkurve, die ein fester Kreispunkt beim Abrollen eines Rades entlang einer Straße erzeugt, und interpretierte diese Kurve als Teil eines Kreisbogens [Cantor 1892, S. 352 ff.]. Galileo Galilei erkannte die besondere Form der Kurve und bezeichnete sie 1599 als Zykloide. Mit Gilles Personne de Roberval (1602-1675) setzte 1634 eine tiefgründige Untersuchung der Zykloide und ihrer Eigenschaften ein, an der sich in der Folge zahlreiche namhafte Mathematiker beteiligten, die aber auch zu Streitigkeiten über die Urheberschaft der Erkenntnisse führte. ([Cantor 1892, S.801 ff.] und [Loria 1911, S. 74 f.])

Geometrische Konstruktion

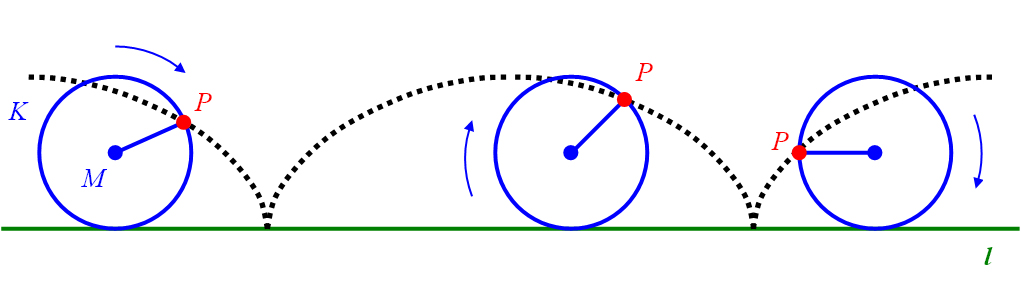
Ein Kreis $K$ mit dem Mittelpunkt $M$ rollt, ohne zu gleiten, auf einer Leitgeraden $l$ ab. Die Bahnkurve, die ein fester Punkt $P$ der Kreislinie durchläuft, wird als gewöhnliche Zykloide bezeichnet (Abbildung 22).

Abbildung 22: Bahnlinie einer gewöhnlichen Zykloide.

Kurvengleichung und Singularitäten

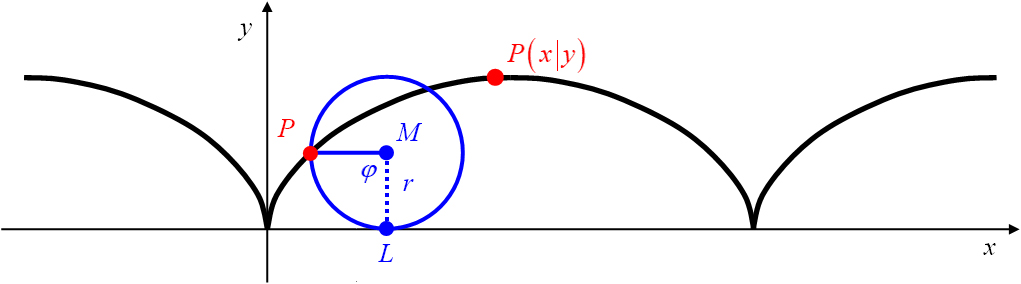
Für die analytische Beschreibung der Zykloide wird ein kartesisches Koordinatensystem so definiert, dass die $x$-Achse mit der Leitgeraden $l$ übereinstimmt und die $y$-Achse einen Tiefpunkt der zykloidalen Bahnkurve enthält (Abbildung 23).

Abbildung 23: Die gewöhnliche Zykloide im Koordinatensystem.

Kennzeichne $L$ immer den Berührungspunkt des Rollkreises $K$ auf der Leitgerade. Mit Hilfe des Zentriwinkels $\angle PML$, der auch als Wälzwinkel $\phi$ bezeichnet wird (Abbildung 23), lässt sich die Lage des Rollkreises eindeutig beschreiben. In Abhängigkeit vom Radius $r$ des Rollkreises und von $\phi$ entstehen dann für die Koordinaten der Bahnkurvenpunkte parametrische Darstellungen:

	Gewöhliche Zykloide:		${\displaystyle x=r\cdot \left(\phi -sin\phi \right)}$       ${\displaystyle y=r\cdot \left(\phi -cos\phi \right)}$
			mit   ${\displaystyle -\mathrm{\infty }<\phi <\mathrm{\infty }}$

Die periodisch auftretenden Tiefpunkte der Zykloidenkurve stellen singuläre Punkte dar, da die Kurve dort in Spitzen ausläuft.

Verkürzte und verlängerte Zykloide

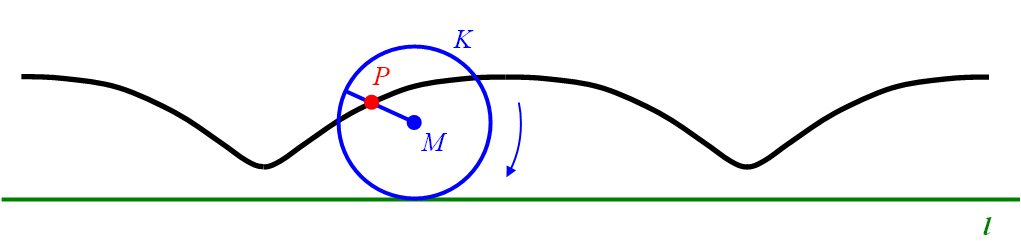
Eine erweitere Sichtweise auf die Zykloide als Rollkurve lässt sich aus einer verallgemeinerte Lage des Punktes $P$ gewinnen. Der Punkt $P$ sei ein fester Punkt in Bezug auf den Rollkreis $K$ mit dem Mittelpunkt $M$. Bezeichne $a$ den Abstand ${\displaystyle \left|\stackrel{\_}{MP}\right|}$. Liegt $P$ innerhalb der Kreisfläche, gilt also $a<r$, so entsteht als Bahnkurve des Punktes $P$ eine verkürzte Zykloide (Abbildung 24).

Abbildung 24: Verkürzte Zykloide.

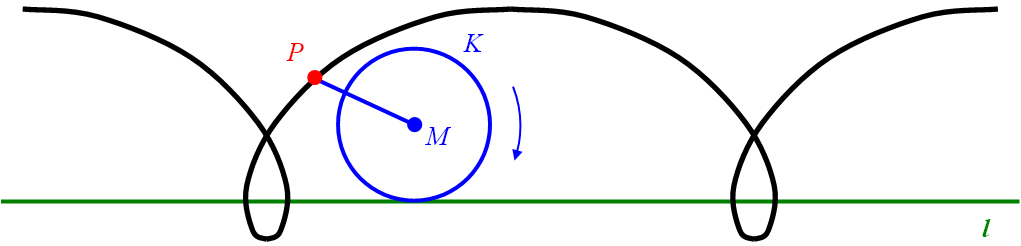
Liegt $P$ außerhalb der Kreisfläche, gilt also $a>r$, so entsteht eine verlängerte Zykloide (Abbildung 25).

Abbildung 25: Verlängerte Zykloide.

In Abhängigkeit vom Wälzwinkel $\phi$ lassen sich die Koordinaten der Kurvenpunkte der verkürzten und verlängerten Zykloide in Parameterform ausdrücken. Die Festlegung des entsprechenden kartesischen Koordinatensystems erfolgt analog zu dem der gewöhnlichen Zykloide.

	Verkürzte bzw. verlängerte Zykloide:		${\displaystyle x=a\cdot \left(\phi -\frac{a}{r}\cdot sin\phi \right)}$       ${\displaystyle y=a\cdot \left(\phi -\frac{a}{r}\cdot cos\phi \right)}$
			mit   ${\displaystyle -\mathrm{\infty }<\phi <\mathrm{\infty }}$   und   ${\displaystyle \frac{a}{r}<1}$   bzw.   ${\displaystyle \frac{a}{r}>1}$

Die verkürzte Zykloide weist keine singulären Punkte auf. Die verlängerte Zykloide besitzt in periodisch wiederkehrender Folge Singularitäten in Form von Doppelpunkten.