Die Archimedische Spirale

Die Entdeckung der Archimedischen Spirale wird verschiedentlich dem griechischen Mathematiker Konon von Samos (ca. 280-240/220 v.u.Z.) und Archimedes (287-212 v.u.Z) selbst zugeschrieben. Unstrittig ist, dass Archimedes die nach ihm benannte Spirallinie erstmals tiefgründig untersuchte und eine Vielzahl geometrischer Zusammenhänge erfasste und beschrieb. ([Hoppe, S. 264 ff.] und [Cantor 1880, S. 262 f.])

Geometrische Konstruktion

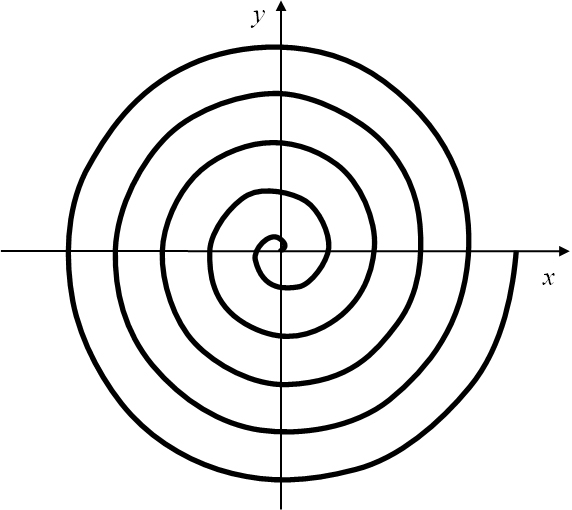
Die Spirale (Abbildung 12) beschreibt Archimedes selbst als Bahnlinie eines Punktes im Resultat zweier gleichförmiger Bewegungen.

"Wenn eine gerade Linie in einer Ebene um einen ihrer Endpunkte, welcher unbeweglich bleibt, mit gleichförmiger Geschwindigkeit sich bewegt, bis sie wieder dahin gelangt, von wo die Bewegung ausging, und wenn zugleich in der bewegten Linie ein Punkt mit gleichförmiger Geschwindigkeit von dem unbewegten Endpunkte anfangend sich bewegt, so beschreibt dieser Punkt eine Schneckenlinie in der Ebene." (zitiert nach: [Cantor 1880, 262 f.])

Abbildung 12: Archimedische Spirale.

Kurvengleichung und geometrische Besonderheiten

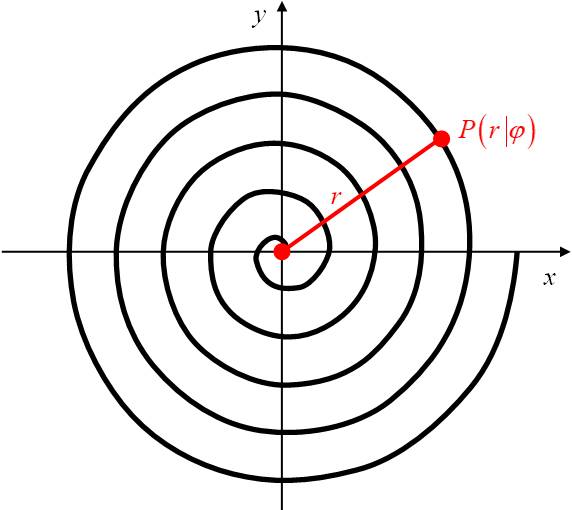
Die einfachste Darstellung einer Kurvengleichung der Archimedischen Spirale erfolgt in Polarkoordinaten (Abbildung 13).

Archimedische Spirale:

${\displaystyle r=k\phi }$       ${\displaystyle \left(0\le \phi <\mathrm{\infty },k>0\right)}$

Die Kurvengleichung beschreibt den Abstand $r$ eines Spiralpunktes vom Pol (die Radialkoordinate) als lineare Funktion des zugehörigen Polarwinkels $\phi$ (die Winkelkoordinate). Die Konstante $k$ charakterisiert die Schrittweite der Archimedischen Spirale. Die Linearität der Kurvengleichung klassifiziert die Archimedische Spirale als eine algebraische Spirale.

Abbildung 13: Archimedische Spirale mit einem Spiralpunkt in Polarkoordinaten.

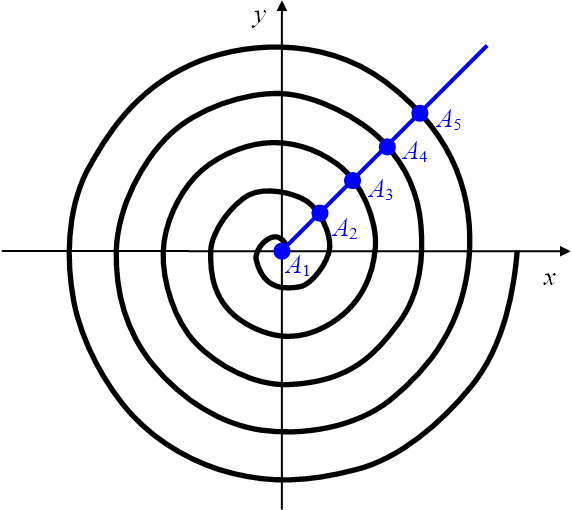
Der Einfluss der Konstante $k$ auf die Spirale wird deutlich, wenn ein Strahl vom Pol aus gezeichnet und die Folge der durch den Strahl erfassten Spiralpunkte $A_1$, $A_2$, $A_3$, ... betrachtet wird (Abbildung 14, rechts). Es gilt für jeweils zwei solcher aufeinanderfolgende Spiralpunkte $\left|\stackrel{\_}{A_i{A}_{i+1}}\right|=2\pi \cdot k$.

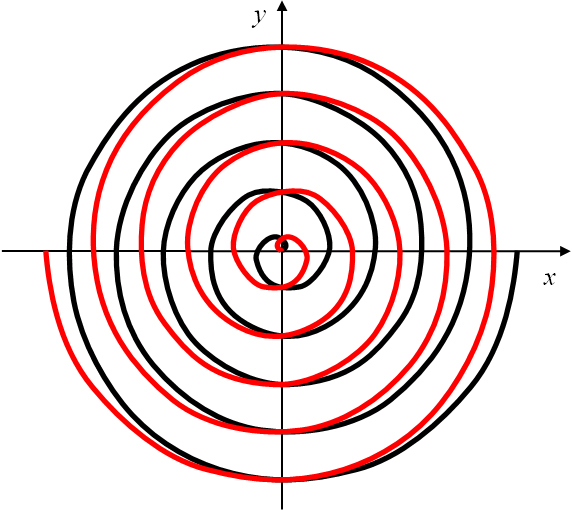
Die Erweiterung der Polarwinkel auf den negativen reellen Bereich $-\mathrm{\infty }<\phi \le 0$ führt mit der Polargleichung ${\displaystyle r=k\left|\phi \right|}$ zur Ausbildung eines zweiten Spiralastes der Archimedischen Spirale, der spiegelsymmetrisch zur $y$-Achse als sekundärer Polarachse verläuft (Abbildung 14, rechts).

Abbildung 14: Archimedische Spirale mit Schrittweite (links) und mit zwei Spiralästen (rechts).