Die logarithmische Spirale

Albrecht Dürer (1471-1528) skizzierte in seiner Unterweysung eine ewige lini und beschrieb diese als eine stetig auf ein Zentrum zulaufende und nach außen nicht endende Kurve, deren Abstand bei jeder vollen Umrundung des Zentrums gleichmäßig nach innen abnimmt und nach außen zunimmt [Dürer, Abbildung 27].

Unabhängig davon beschrieb 1638 René Descartes (1596-1650) in einem Brief an Marin Mersenne (1588-1648) die Eigenschaften einer Spirale. Die Struktur ihrer polaren Kurvengleichung veranlasste Pierre de Varignon (1654-1722), diese Spirale als logarithmische Spirale zu bezeichnen [Loria 1911, S. 61].

Geometrische Konstruktion

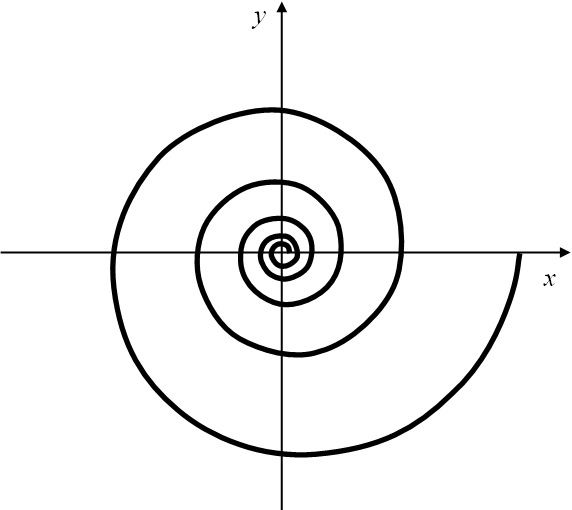
Eine logarithmische Spirale (Abbildung 17) entsteht als Bahnlinie eines Punktes im Resultat zweier Bewegungen: einer gleichförmige Drehbewegung und einer beschleunigten Bewegung, deren Geschwindigkeit gleichmäßig zunimmt.

Eine Gerade bewege sich in einer Ebene um einen ihrer Geradenpunkte, welcher unbeweglich bleibt, mit gleichförmiger Geschwindigkeit. Gleichzeitig entferne sich ein zweiter Geradenpunkt von dem unbeweglichen Punkt mit einer Geschwindigkeit, die dem Abstand der beiden Punkte proportional sei. Der bewegliche Geradenpunkt beschreibt eine Kurvenlinie, die als logarithmische Spirale bezeichnet wird (nach [Wygodski, S. 731]).

Abbildung 17: Logarithmische Spirale.

Kurvengleichung und geometrische Besonderheiten

Die Kurvengleichung einer logarithmischen Spirale stellt sich für den Abstand $r$ eines Spiralpunktes vom Pol als Exponentialfunktion des Polarwinkels $\phi$ oder für den Polarwinkel als Logarithmus des Abstandes dar. Diese Beziehung führt zur Bezeichnung als logarithmische Spirale.

	Logarithmische Spirale:		${\displaystyle r=a{e}^{k\phi }}$	${\displaystyle \left(-\mathrm{\infty }<\phi <\mathrm{\infty },a>0,k\in \mathrm{ℝ}\right)}$
			${\displaystyle \phi =\frac{1}{k}ln\frac{r}{a}}$	${\displaystyle \left(r>0,a>0,k\ne 0\right)}$

Die Konstante $a$ ist der Polarradius des Spiralpunktes mit $\phi =0$ und stellt somit den Ursprungsabstand des spiralerzeugenden Punktes vom Polarzentrum dar. Die Konstante $k$ kennzeichnet in der Exponentialgleichung die Zuwachsrate, mit der sich die Spiralpunkte vom Zentrum entfernen oder dem Zentrum asymptotisch annähern. Die Größe von $k$ führt zur Ausbildung einer Linksspirale für $k>0$ und einer Rechtsspirale für $k<0$. Mit $k=0$ entartet die Spirale zu einem Kreis.

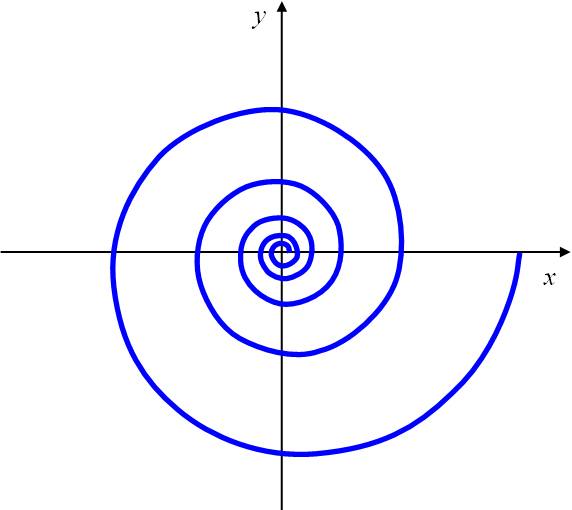
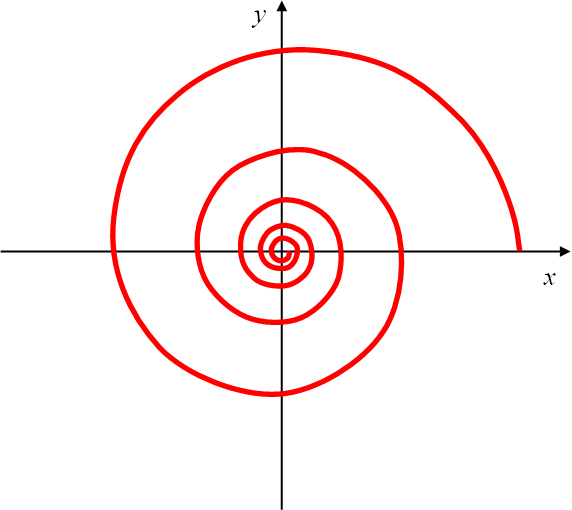
Bei einer Linksspirale nimmt der Abstand der Spiralpunkte vom Zentrum mit wachsendem Polarwinkel zu und für große negative Polarwinkel ist das Zentrum ein asymptotischer Punkt (Abbildung 18, links). Bei einer Rechtsspirale nähern sich die Spiralpunkte mit wachsendem Polarwinkel dem Zentrum asymptotisch an und für negative Polarwinkel entfernen sich die Spiralpunkte vom Zentrum (Abbildung 18, rechts).

Abbildung 18: Logarithmische Spirale als Linksspirale mit $k>0$ (links) und als Rechtsspirale mit $k<0$ (rechts).

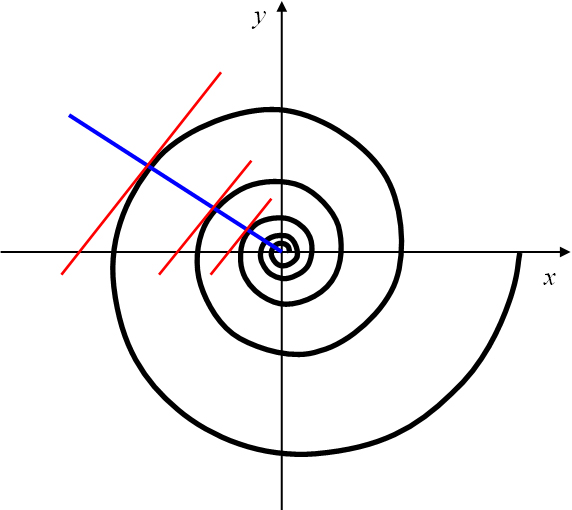
Eine charakteristische Eigenschaft der logarithmischen Spirale ist die Parallelität der Tangenten an die Spiralpunkte, die auf einem vom Zentrum ausgehenden Strahl liegen (Abbildung 19). Der Schnittwinkel aller vom Zentrum ausgehenden Strahlen mit den jeweiligen Spiraltangenten ist konstant und lässt sich mit der Größe ${\displaystyle arctan\frac{1}{k}}$ bestimmen. Diese spiraldefinierende Eigenschaft führte auch zur Bezeichnung der logaithmischen Spirale als gleichwinklige Spirale ([Loria 1911, S. 61]).

Abbildung 19: Die Tangenten an die auf einem Zentrumsstrahl liegenden Spiralpunkte sind parallel.