Die hyperbolische Spirale

Die hyperbolische Spirale wurde unabhäbgig voneinander durch Pierre de Varignon (1654-1722) und Johann Bernoulli (1667-1748) entdeckt und beschrieben. Die Bezeichnung der Spiralform als hyperbolisch resultiert aus der Analogie der Kurvengleichung in Polarkoordinaren zur Kurvengleichung der Hyperbel in kartesischen Koordinaten [Loria 1911, S. 55].

Geometrische Beschreibung

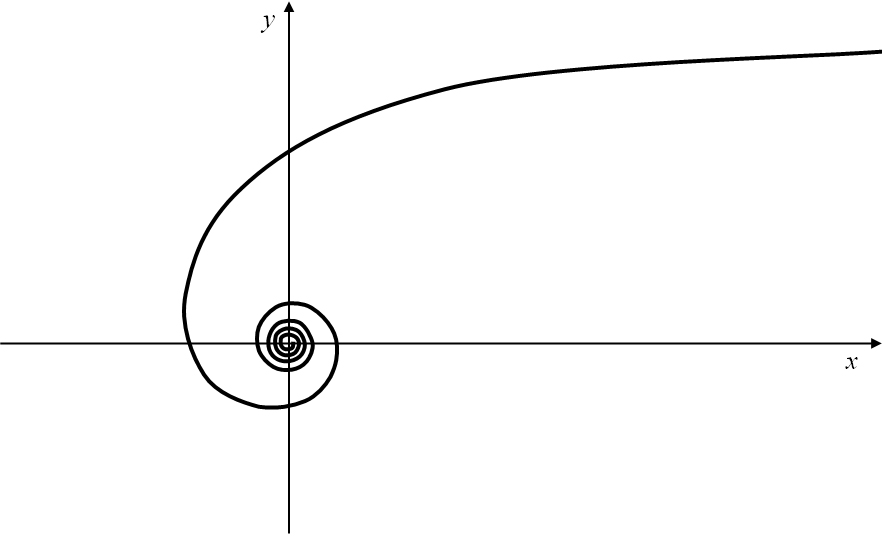
Eine hyperbolische Spirale (Abbildung 15) ist charakterisiert durch die indirekte Proportionaltät zwischen dem Polarwinkel eines Kurvenpunktes und dem Abstand des Kurvenpunktes von polaren Zentrum. Für sehr kleine Polarwinkel sind die Kurvenpunkte nahezu unendlich weit vom Zentrum entfernt und zeigen ein asymptotisches Verhalten. Je größer der Winkel wird, desto enger wird das Zentrum von der Kurvenlinie umschlossen; die Spirale nähert sich dem Zentrum asymptotisch an.

Abbildung 15: Hyperbolische Spirale.

Kurvengleichung und geometrische Besonderheiten

Die Kurvengleichung einer hyperbolischen Spirale lässt sich am einfachsten in Polarkoordinaten darstellen.

Hyperbolische Spirale:

${\displaystyle r=\frac{a}{\phi }}$       ${\displaystyle \left(0<\phi <\mathrm{\infty },a>0\right)}$

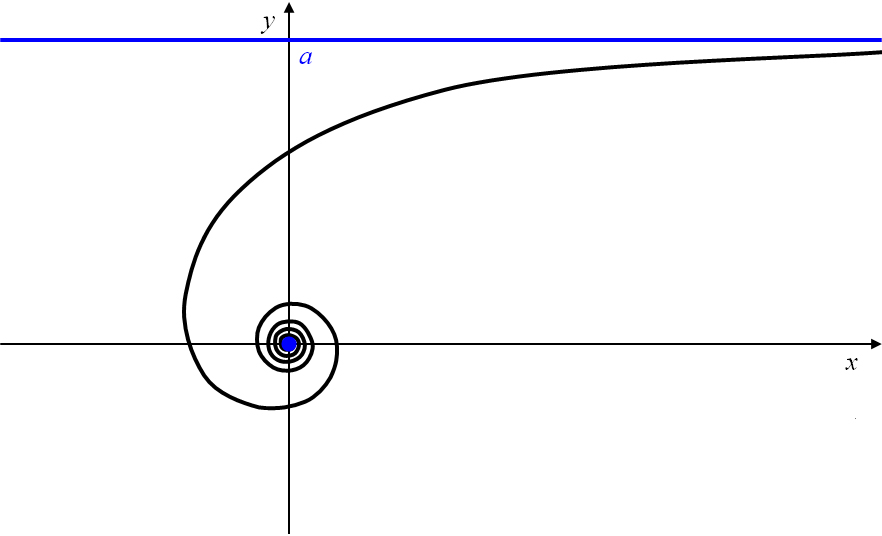
Die Kurvengleichung beschreibt den Abstand $r$ eines Spiralpunktes vom Pol als Reziproke des zugehörigen Polarwinkels $\phi$. Die Konstante $a$ definiert die Lage der Asymptote, der sich die Spiralpunkte mit immer kleiner werdenden Polarwinkeln annähern (Abbildung 16). Die Gestalt der Kurvengleichung als polynomiale Gleichung klassifiziert die hyperbolische Spirale als eine algebraische Spirale.

Abbildung 16: Hyperbolische Spirale mit Zentrum und Asymptote.

Der Nachweis für die Existenz der Asymptote lässt sich durch eine Transformation der Polarkoordinaten in kartesische Koordinaten führen. Die entsprechenden Transformationsgleichungen sind $x=r\cdot cos\phi$ und $y=r\cdot sin\phi$.

Das Einsetzen der hyperbolischen Beziehung ${\displaystyle r=\frac{a}{\phi }}$ in die Transformationsgleichungen führt zu ${\displaystyle x\left(\phi \right)=\frac{a\cdot cos\phi }{\phi }}$ und zu ${\displaystyle y\left(\phi \right)=\frac{a\cdot sin\phi }{\phi }}$. Damit folgt ${\displaystyle \underset{\phi \to 0}{\overset{\mathrm{}}{lim}}x\left(\phi \right)=\underset{\phi \to 0}{\overset{\mathrm{}}{lim}}\frac{a\cdot cos\phi }{\phi }=\mathrm{\infty }}$ sowie ${\displaystyle \underset{\phi \to 0}{\overset{\mathrm{}}{lim}}y\left(\phi \right)=\underset{\phi \to 0}{\overset{\mathrm{}}{lim}}\frac{a\cdot sin\phi }{\phi }=a}$.