Die Klothoide

Jakob Bernoulli (1654-1705) beschrieb 1694 die Gleichung einer Kurve mit der charakteristischen Eigenschaft, dass die Krümmung der Kurve an einem Kurvenpunkt direkt proprtional zur Länge des Kurvenbogens bis zu diesem Kurvenpunkt ist. Unabhängig voneinander entdeckten 1743 Leonard Euler (1707-1783) und 1874 Marie Alfred Cornu (1841-1902) die Gleichungen dieser Spiralkurve erneut und stellten sie numerisch und graphisch dar. Der italienische Mathematiker Ernesto Cesàro (1859-1906) führte in Anlehnung an das Aussehen einer Spinnrolle die Bezeichnung der Spirale als Klothoide (Spinnlinie) ein und formulierte wesentliche Eigenschaften der Spirale. ([Loria 1911, S. 70 ff.] und [Archibald, S. 276 ff.])

Geometrische Beschreibung

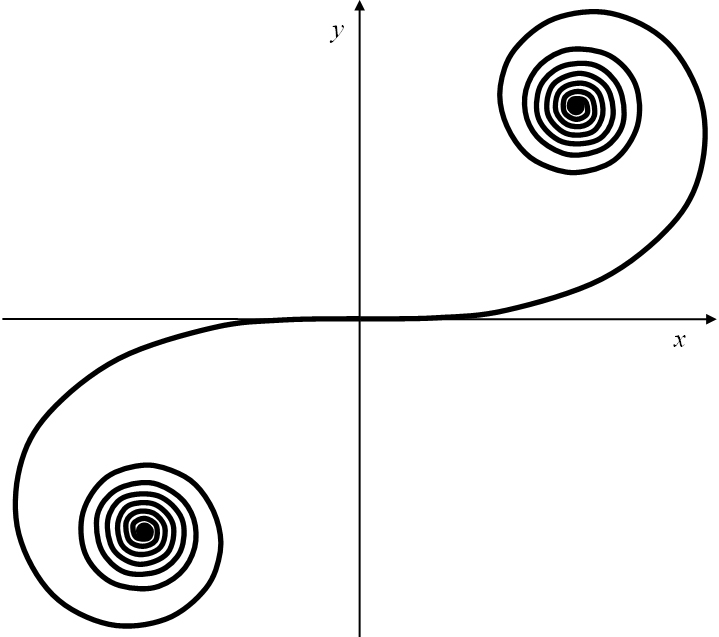
Eine Klothoide (Abbildung 20) besteht aus zwei zum Polarzentrum punktsymmetrischen Spiralästen, die sich mit wachsendem Betrag des Polarwinkels jeweils einem Punkt asymptotisch nähern. Die Spiraläste verlaufen im Zentrum tangential zur Polarachse.

Abbildung 20: Klothoide.

Kurvengleichungen und geometrische Besonderheiten

Die Koordinaten der Klothoidenpunkte lassen sich aus der Proportionalität zwischen der Kurvenkrümmung in einem Kurvenpunkt zur Länge des Bogens $s$ bis zu diesem Punkt ableiten. Es ergibt sich eine parametrische Darstellung für die kartesischen Koordinaten der Klothoidenpunkte.

	Klothoide:		${\displaystyle x=a\sqrt{\mathrm{\pi }}\underset{0}{\overset{t}{\int }}cos\left(\frac{\mathrm{\pi }{u}^2}{2}\right)du}$
			${\displaystyle y=a\sqrt{\mathrm{\pi }}\underset{0}{\overset{t}{\int }}sin\left(\frac{\mathrm{\pi }{u}^2}{2}\right)du}$
			mit   ${\displaystyle t=\frac{s}{a\sqrt{\mathrm{\pi }}}}$   und   ${\displaystyle -\mathrm{\infty }<t<\mathrm{\infty }}$

Die Konstante $a$ kennzeichnet den Proportionalitätsfaktor ${\displaystyle \frac{1}{a^2}}$ zwischen der Krümmung und der Bogenlänge. Die Integrale in den Parametergleichungen werden auch als Fresnel-Integrale, nach Augustin Jean Fresnel (1788-1827), bezeichnet. ([Loria 1911, S. 70 ff.]).

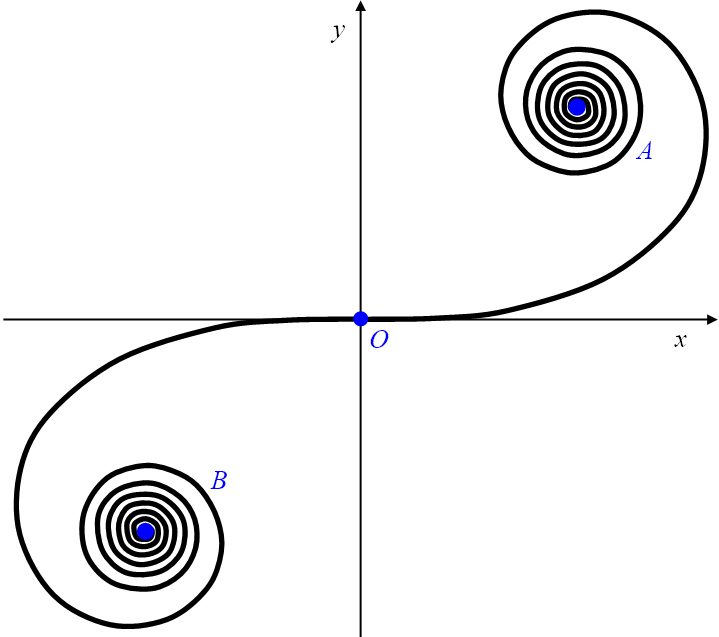
Die beiden Spiraläste der Klothoide sind symmetrisch in Bezug auf den Koordinatenursprung, damit liegt in $O$ ein Symmetriezentrum vor. Für immer größer werdende Parameterwerte $t$ nähern sich die Klothoidenpunkte asymptotisch dem Punkt ${\displaystyle A\left(\frac{a\sqrt{\mathrm{\pi }}}{2}|\frac{a\sqrt{\mathrm{\pi }}}{2}\right)}$ an. Mit der Punktsymmetrie der Klothoide existiert in ${\displaystyle B\left(-\frac{a\sqrt{\mathrm{\pi }}}{2}|-\frac{a\sqrt{\mathrm{\pi }}}{2}\right)}$ ein zweiter Asymptotenpunkt für große negative Parameterwerte $t$ (Abbildung 21).

Abbildung 21: Klothoide mit Symmetriezentrum $O$ und den asymptotischen Punkten $A$ und $B$.