Das Ellipsoid

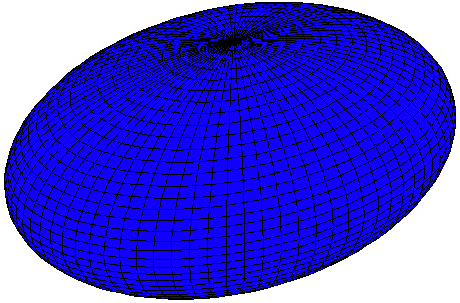
Ein Ellipsoid (Abbildung) ist eine reguläre Fläche zweiter Ordnung. Der Name der Fläche entstammt dem Griechischen und bedeutet "eine Ellipse zeigend". Damit wird Bezug genommen auf die Form der Schnittfiguren, die entstehen, wenn das Ellipsoid mit Ebenen parallel zu jeweils zwei Hauptachsen geschnitten wird: es entstehen Ellipsen.

Abbildung: Ellipsoid mit der Flächengleichung   $x^2+2y^2+4z^2-4=0$

Die allgemeine Flächengleichung eines Ellipsoid in Normalform lautet   $a·x^2+b·y^2+c·z^2+d=0$   mit $a,b,c>0$ und $d<0$. Die Normalform liegt genau dann vor, wenn die Hauptachsen des Ellipsoids mit den Koordinatenachsen zusammenfallen.

Die Flächengleichung in Normalform kann mit Division durch $d$ in eine Gleichung   $\frac{x^2}{p^2}+\frac{y^2}{q^2}+\frac{z^2}{r^2}=1$   umgeformt werden. Aus dieser Gleichung lassen sich die Längen der großen Halbachsen des Ellipsoid mit $p,q,r$ direkt ablesen.

Sind alle drei großen Halbachsen gleichlang, liegt also ein Ellipsoid der Form   $x^2+y^2+z^2=R^2$   vor, so geht das Ellipsoid in eine Kugel über (genauer in eine Kugelfläche) mit dem Radius $R$. Als Schnittfiguren parallel zu jeweils zwei Hauptachsen entstehen Kreise.

Ein Ellipsoid, bei dem zwei große Halbachsen die gleiche Länge aufweisen und die Länge der dritten großen Halbachse verschieden davon ist, wird als Rotationsellipsoid oder als Sphäroid bezeichnet. Alle Schnitte parallel zu den beiden gleichen Halbachsen ergeben Kreise als Schnittfiguren.