Das hyperbolische Paraboloid

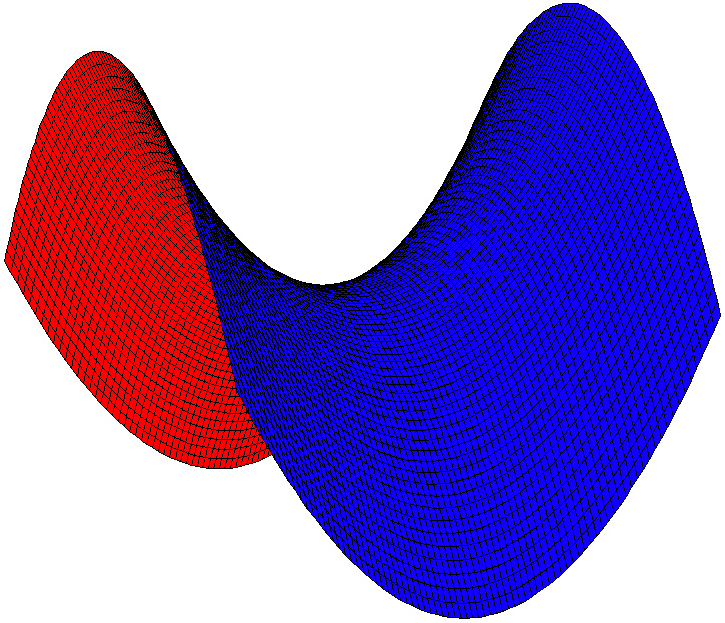
Ein hyperbolisches Paraboloid (Abbildung) ist eine singuläre Fläche zweiter Ordnung. Die Fläche wird auch als Sattelfläche bezeichnet, da sie in zwei Hauptrichtungen entgegengesetzt gekrümmt ist und somit die die typische Form eines Sattels annimmt. Liegt das Paraboloid in Normalform vor (d.h. die Hauptachsen der Fläche fallen mit den Koordinatenachsen zusammen), so entstehen in zwei Koordinatenrichtungen Parabeln als Schnittfiguren von Ebenen parallel zu den Koordinatenebenen. Diese Parabeln führen zur Bezeichnung der Fläche als Paraboloid, dem griechischen Namen folgend "eine Parabel zeigend". Die Schnittfiguren in Richtung der dritten Koordinate sind Hyperbeln.

Die Bezeichnung als hyperbolisches Paraboloid unterscheidet diese Fläche zweiter Ordnung vom elliptischen Paraboloid, bei dem als Schnittfiguren in die dritte Koordinatenrichtung Ellipsen entstehen.

Abbildung: Hyperbolisches Paraboloid mit der Flächengleichung   $x^2-y^2-z=0$

Die allgemeine Flächengleichung eines hyperbolischen Paraboloids in Normalform lautet   $a\cdot x^2+b\cdot y^2+c\cdot z=0$  
mit , und $c\ne 0$. Das hyperbolische Paraboloid unterscheidet sich in der Normalformgleichung also nur im Vorzeichen des Parameters $b$ vom elliptischen Paraboloid.

Die Parabeln, die als Schnittfiguren des hyperbolischen Paraboloids in der Normalform mit der $x$-$z$- bzw. $y$-$z$-Koordinatenebene entstehen, werden als Hauptschnitte des Paraboloids bezeichnet.

Die in der Normalform als lineares Glied auftretende $z$-Koordinate markiert diejenige Hauptachse, in deren Richtung senkrecht zur Achse die Hyperbeln als Ebenenschnitte entstehen. Diese Hauptachse wird auch nur als Achse des Paraboloids bezeichnet. Erfolgt der Ebenenschnitt oberhalb der $x$-$y$-Koordinatebene, liegen die Scheitel der Hyperbel auf einer Parallelen zur $x$-Achse. Erfolgt der Ebenenschnitt unterhalb der der $x$-$y$-Koordinatenebene, liegen die Hyperbelscheitel auf einer Parallelen zur $y$-Achse.

Der Ebenenschnitt in der $x$-$y$-Koordinatebene, senkrecht zur $z$-Achse, liefert als Schnittfigur ein Geradenpaar mit den Geradengleichungen $y=\sqrt{-\frac{a}{b}}\cdot x$ und $y=-\sqrt{-\frac{a}{b}}\cdot x$. Diese beiden Geraden werden Scheitelgeraden genannt. Die beiden Scheitelgeraden bilden jede für sich mit der $z$-Achse eine Ebene. Diese beiden Ebenen werden als Richtebenen bezeichnet. Sie schneiden aus den senkrecht zur $z$-Achse liegenden Schnittebenen die Asymptoten der Schnitthyperbeln aus.

Das mit der Normalform beschreibene hyperbolische Paraboliod hat im Koordinatenursprung seinen Scheitelpunkt als Schnittpunkt der beiden Scheitelgeraden. Der Scheitel eines hyperbolischen Paraboloids ist ein Sattelpunkt der Fläche, d.h. ein Punkt ohne Steigung und Krümmung.

Die Flächengleichung in Normalform kann mit Division durch $-\frac{c}{2}$ in eine Gleichung   $\frac{x^2}{p^2}-\frac{y^2}{q^2}-2z=0$   umgeformt werden. Aus dieser Gleichung lassen sich mit $p^2$ und $q^2$ die Halbparameter der Hauptschnittparabeln direkt ablesen.

Das hyperbolische Paraboloid ist die einzige echte Fläche 2. Ordnung, die in keinem Fall als eine Rotationsfläche dargestellt werden kann. Zudem weist sie als einzige echte Fläche 2. Ordnung keine Drehsymmetrie auf. Die $x$-$z$- bzw. $y$-$z$-Koordinatenebenen stellen Symmetrieebenen (Spiegelebenen) des Paraboloids dar.

Für jedes hyperbolische Paraboloid der Form   $\frac{x^2}{p^2}-\frac{y^2}{q^2}-2z=0$   lassen sich zwei Scharen geradliniger Erzeugender feststellen. Als geradlinige Erzeugende einer Fläche wird eine Gerade bezeichnet, die ganz in der Fläche liegt. Die Gleichungen dieser Geradenscharen ergeben sich als Schnitte zweier Ebenenscharen:

Erzeugendenschar I	$\frac{x}{p}+\frac{y}{q}=u$	$u\cdot \left(\frac{x}{p}-\frac{y}{q}\right)=2z$
Erzeugendenschar II	$\frac{x}{p}-\frac{y}{q}=v$	$v\cdot \left(\frac{x}{p}+\frac{y}{q}\right)=2z$

Die Parameter $u$ und $v$ sind beliebige reelle Zahlen. Durch jeden Flächenpunkt des hyperbolischen Paraboloids verlaufen zwei Geraden: eine Erzeugende der Schar I und eine Erzeugende der Schar II.