Das zweischalige Hyperboloid

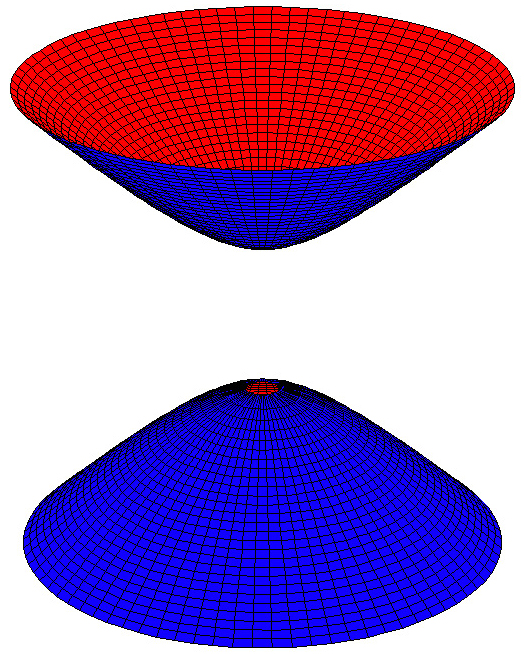
Ein zweischaliges Hyperboloid (Abbildung) ist eine reguläre Fläche zweiter Ordnung, die aus zwei nichtzusammenhängenden Teilflächen (Schalen) besteht. Liegt das Hyperboloid in Normalform vor (d.h. die Hauptachsen der Fläche fallen mit den Koordinatenachsen zusammen), so entstehen Hyperbeln als Schnittfiguren von Ebenen parallel zu den Koordinatenebenen, in zwei Koordinatenrichtungen gesehen. Diese Hyperbeln verleihen dem Hyperboloiden den griechischen Namen: "eine Hyperbel zeigend". Die Schnittfiguren in Richtung der dritten Koordinate sind Ellipsen.

Abbildung: Zweischaliges Hyperboloid mit der Flächengleichung   $x^2+y^2-z^2+1=0$

Die allgemeine Flächengleichung eines zweischaligen Hyperboloids in Normalform lautet   $a·x^2+b·y^2+c·z^2+d=0$   mit $a,b,d>0$ und $c<0$. Das zweischalige Hyperboloid unterscheidet sich in der Normalformgleichung also nur im Vorzeichen des Absolutgliedes $d$ vom einschaligen Hyperboloid.

In der Normalform wird das zweischalige Hyperboloid so ausgerichtet, dass die Schnittfiguren der Schalen mit Ebenen in $z$-Richtung, parallel zur $x$-$y$-Koordinatenebene, die Ellipsen sind. Die Hyperbeln, die als Schnittfiguren des zweischaligen Hyperboloids mit der $x$-$z$- bzw. $y$-$z$-Koordinatenebene entstehen, werden als Hauptschnitte bezeichnet.

Die Flächengleichung in Normalform kann mit Division durch $d$ in eine Gleichung   $\frac{x^2}{p^2}+\frac{y^2}{q^2}-\frac{z^2}{r^2}=-1$   umgeformt werden. Aus dieser Gleichung lassen sich mit $p$ und $r$ bzw. mit $q$ und $r$ die Scheitelachsen der Hyperbeln der Hauptschnitte parallel zur $z$-Achse direkt ablesen. Jeder Schnitt senkrecht zur $z$-Achse mit $\left|z\right|>r$ liefert eine Ellipse als Schnittfigur. Gilt $p=q$, so liegt ein zweischaliges Rotationshyperboloid vor.