Das elliptische Paraboloid

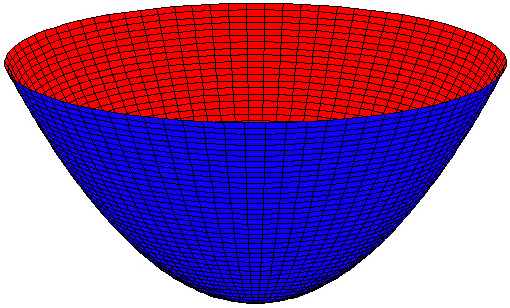
Ein elliptisches Paraboloid (Abbildung) ist eine singuläre Fläche zweiter Ordnung. Liegt das Paraboloid in Normalform vor (d.h. die Hauptachsen der Fläche fallen mit den Koordinatenachsen zusammen), so entstehen in zwei Koordinatenrichtungen Parabeln als Schnittfiguren von Ebenen parallel zu den Koordinatenebenen. Diese Parabeln führen zur Bezeichnung der Fläche als Paraboloid, dem griechischen Namen folgend "eine Parabel zeigend". Die Schnittfiguren in Richtung der dritten Koordinate sind Ellipsen.

Die Bezeichnung als elliptisches Paraboloid unterscheidet diese Fläche zweiter Ordnung vom hyperbolischen Paraboloid, bei dem als Schnittfiguren in die dritte Koordinatenrichtung Hyperbeln entstehen.

Abbildung: Elliptisches Paraboloid mit der Flächengleichung   $x^2+y^2-z=0$

Die allgemeine Flächengleichung eines elliptischen Paraboloids in Normalform lautet   $a\cdot x^2+b\cdot y^2+c\cdot z=0$  
mit $a,b>0$ und $c\ne 0$.

Die in der Normalform nur als lineares Glied auftretende $z$-Koordinate markiert diejenige Hauptachse, in deren Richtung die Ellipsen als Ebenenschnitte entstehen. Zugleich ist sie als Symmetrieachse des Paraboloids ausgezeichnet, und sie wird auch als Achse des Paraboloids bezeichnet. Die Parabeln, die als Schnittfiguren des elliptischen Paraboloids mit der $x$-$z$- bzw. $y$-$z$-Koordinatenebene entstehen, werden als Hauptschnitte des Paraboloids benannt. Der Ursprung des Paraboloids heißt Scheitel.

Die Flächengleichung in Normalform kann mit Division durch $-\frac{c}{2}$ in eine Gleichung   $\frac{x^2}{p^2}+\frac{y^2}{q^2}-2z=0$   umgeformt werden. Aus dieser Gleichung lassen sich mit $p^2$ und $q^2$ die Halbparameter der Hauptschnittparabeln direkt ablesen. Für den Fall $p=q$ liegt ein Rotationsparaboloid vor, die Ebenenschnitte senkrecht zur $z$-Achse ergeben dann Kreise als Schnittfiguren.