Die Parabel

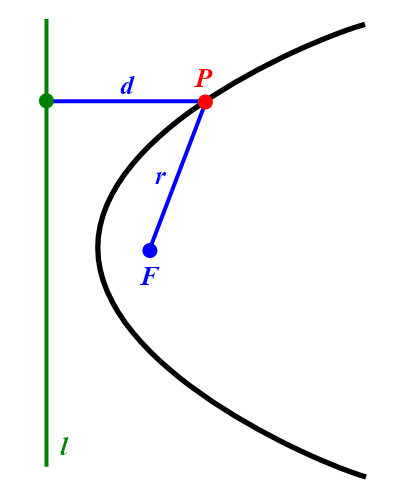
Eine Parabel ist die Menge aller Punkte $P$ einer Ebene, die von einem festen Punkt (Brennpunkt) $F$ und von einer festen Gerade (Leitlinie) $l$ den gleichen Abstand haben (Abbildung 25).

Abbildung 25: Parabel mit Brennpunkt und Leitlinie.

Sei $r=\left|\stackrel{\_}{PF}\right|$ und sei $d$ der Abstand des Punktes $P$ zu der Leitlinie $l$, dann gilt für alle Parabelpunkte $r=d$ bzw. ${\displaystyle \frac{r}{d}=\epsilon =1}$. Der konstante Wert $\epsilon =1$ wird als numerische Exzentrizität bezeichnet.

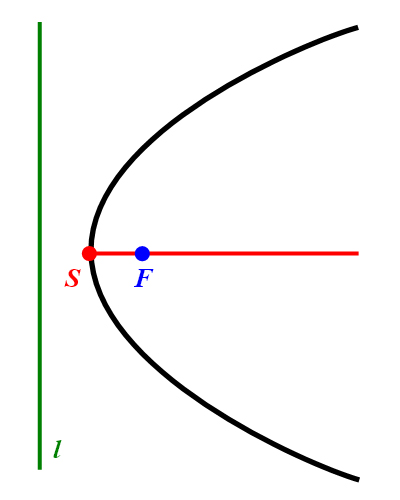
In einer Parabel ist als Mittelpunkt der Abstandsstrecke zwischen Brennpunkt und Leitlinie ein Scheitelpunkt $S$ ausgezeichnet (Abbildung 26, links). Die Halbgerade, die, im Scheitelpunkt $S$ beginnend, durch den Brennpunkt $F$ verläuft, wird Achse der Parabel genannt. Sie ist die einzige Symmetrieachse der ebenen Figur.

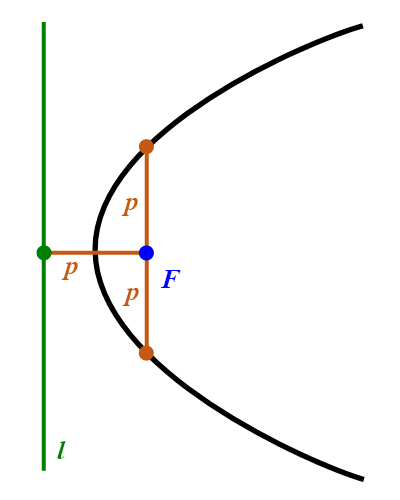
Die Länge $p$ der halben Parabelsehne, die senkrecht zur Parabelachse durch den Brennpunkt $F$ verläuft, stimmt mit dem Abstandes des Brennpunktes $F$ von der Leitline $l$ überein. Diese Länge heißt Halbparameter $p$ der Parabel (Abbildung 26, rechts).

Abbildung 26: Parabel mit Scheitel und Parabelachse (links) und mit Halbparameter (rechts).