Die analytische Beschreibung einer Parabel

Aus der geometrischen Definition über Brennpunkt und Leitlinie lässt sich eine analytische Gleichung einer Parabel in der Normalform ableiten.

Hierfür wird der Parabel ein kartesisches Koordinatensystem derart einbeschrieben, dass der Koordinatenursprung in den Scheitelpunkt der gelegt wird und dass die Abszissenachse mit der Parabelachse zusammenfällt (Abbildung 27).

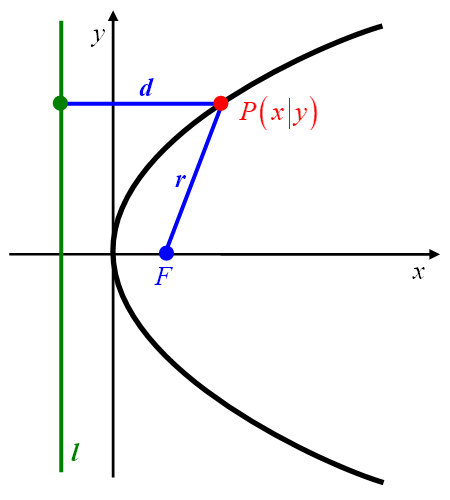
Abbildung 27: Parabel als Kurve im Koordinatensystem.

Die Ordinatenachse verläuft damit parallel zur Leitlinie, der Brennpunkt hat die Koordinaten ${\displaystyle F\left(\frac{p}{2}|0\right)}$ und die Leitlinie genügt der Geradengleichung ${\displaystyle x=-\frac{p}{2}}$.

Mit Hilfe der Markierung der Abszissenlänge $x$ und der Ordinatenlänge $y$ des allgemeinen Parabelpunktes $P\left(x|y\right)$ lässt sich ein rechtwinkliges Dreieck über der Abszissenachse erzeugen (Abbildung 28). Nach dem Satz des Pythogoras gilt für die Abstandslänge $r$ als Hypotenuse des Dreiecks die Gleichung ${\displaystyle r^2={\left(x-\frac{p}{2}\right)}^2+y^2}$. Die Abstandslänge $d$ des Punktes $P$ von der Leitlinie $l$ lässt sich nach der Wahl des Koordinatensystems beschreiben als ${\displaystyle d={\left(x+\frac{p}{2}\right)}^2}$.

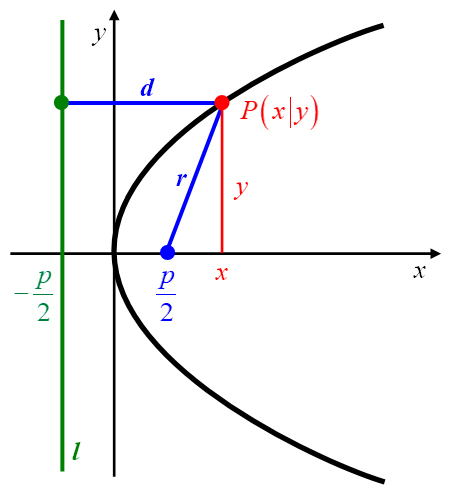
Abbildung 28: Parabel mit Dreieckszerlegung.

Aus der Abstandsgleicheit der Parabelpunkte vom Brennpunkt und der Leitlinie wird durch Einsetzen der obigen Gleichungen, durch Umformen und fortgesetztes Vereinfachen die Parabelgleichung in der Normalform gewonnen:

$${\displaystyle \begin{array}{rcll}r& =& d& \\ {\displaystyle {\left(x-\frac{p}{2}\right)}^2+y^2}& =& {\displaystyle {\left(x+\frac{p}{2}\right)}^2}& \\ {\displaystyle x^2-px+\frac{p^2}{4}+y^2}& =& {\displaystyle x^2+px+\frac{p^2}{4}}& {\displaystyle |-x^2-\frac{p^2}{4}+px}\\ y^2& =& 2px& \end{array}}$$

Im Ergebnis der analytischen Betrachtungen wurde aus der geometrischen Definition der Parabel durch äquivalentes Umformen eine Kurvengleichung abgeleitet, die die Normalform der Parabelgleichung als Kegelschnittgleichung darstellt, mit Angabe des Halbparameters. Die Äquivalenz der geometrischen Definition und der analytischen Definition der Parabel mittels Kegelschnittgleichung und mithin als Kurve zweiter Ordnung wurde somit bewiesen.