Die Parabel als Kegelschnitt

Die Definition der Parabel als geometrische Figur der Ebene erfolgt über den Abstand der Parabelpunkte zum Brennpunkt und zu der Leitlinie der Parabel. Herzustellen ist nunmehr der Zusammenhang zwischen der Betrachtung der Parabel als Schnittfigur am Doppelkegel und ihrer geometrischen Definition. Dieser Zusammenhang kann nachgewiesen werden mit Hilfe einer Dandelinschen Kugel (benannt nach Germinal Pierre Dandelin, 1794-1847), die in den Kegel einbeschrieben wird.

Ein gerader Kreiskegel werde derart von einer Ebene E geschnitten, dass diese die Kegelspitze nicht enthält und dass sie parallel zu einer Mantellinie $m$ verläuft. Die dabei entstehende ebene Schnittfigur soll auf ihre geometrischen Eigenschaften hin untersucht werden.

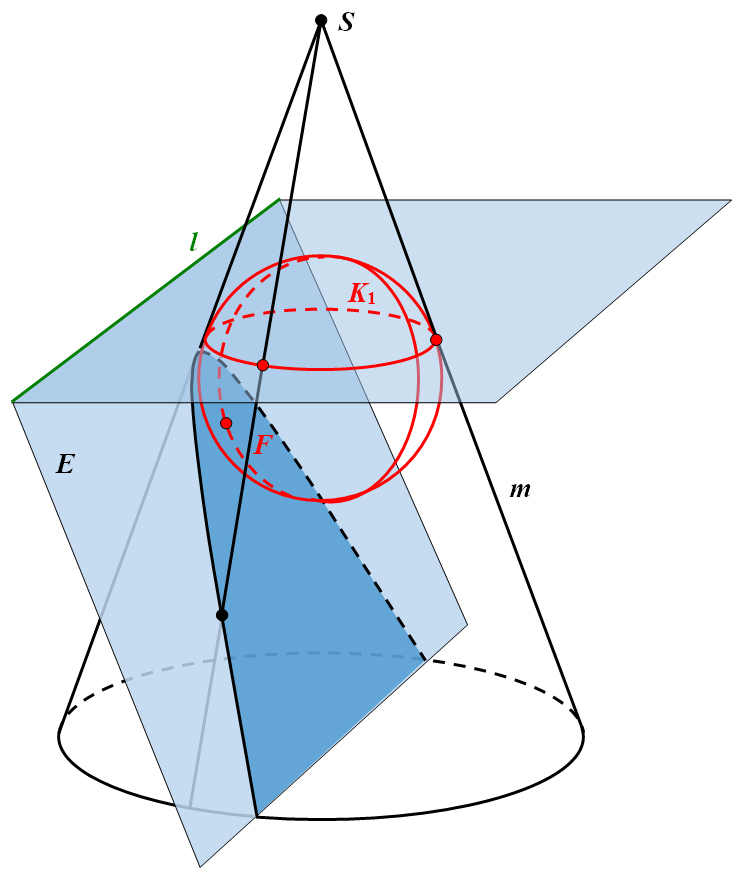
In den Kegel wird zwischen der Kegelspitze $S$ und der Schnittebene $E$ derart eine Dandelinsche Kugel mit dem Mittelpunkt auf der Kegelachse einbeschrieben, dass diese die Schnittebene in genau einem Punkt $F$ und den Kegel auf einer Kreislinie $K_1$ berührt (Abbildung 29). Aufgrund der Symmetrie des geraden Kegels und der Kugel liegt die Kreisebene des horizontalen Berührungskreises senkrecht zur Kegelachse.

Die Schnittebene $E$ und die Kreisebene $K_1$ schneiden sich infolge ihrer Lage in einer Geraden $l$, die orthogonal und windschief zur Kegelachse und auch orthogonal und windschief zur Mantellinie $m$ verläuft.

Abbildung 29: Dandelinsche Kugel am Doppelkegel.

Es sei $P$ ein allgemeiner Punkt der Schnittfigur. Der Punkt $P$ liegt auf einer Mantellinie $m_P$ des geraden Kreiskegels. Auf dieser Mantellinie $m_P$ liegt auch ein Berührungspunkt $A$ des Kreises $K_1$. Die Strecken $\stackrel{\_}{PF}$ und $\stackrel{\_}{PA}$ sind damit Tangentenabschnitte über derselben Kugel und vom selben Punkt ausgehend, es gilt somit für jeden Punkt $P$ der Schnittfigur $\left|\stackrel{\_}{PF}\right|=\left|\stackrel{\_}{PA}\right|$.

Bezeichne $K_2$ den Horizontalkreis des Kegelmantels durch den Punkt $P$. Die beiden Kreisebenen $K_1$ und $K_2$ liegen senkrecht zur Kegelachse und sind parallel zueinander. Sei $Q$ der gemeinsame Punkt des Kreises $K_2$ mit der Mantellinie $m$. Auf der Mantellinie $m$ liegt auch ein Berührungspunkt $B$ des Kreises $K_1$.

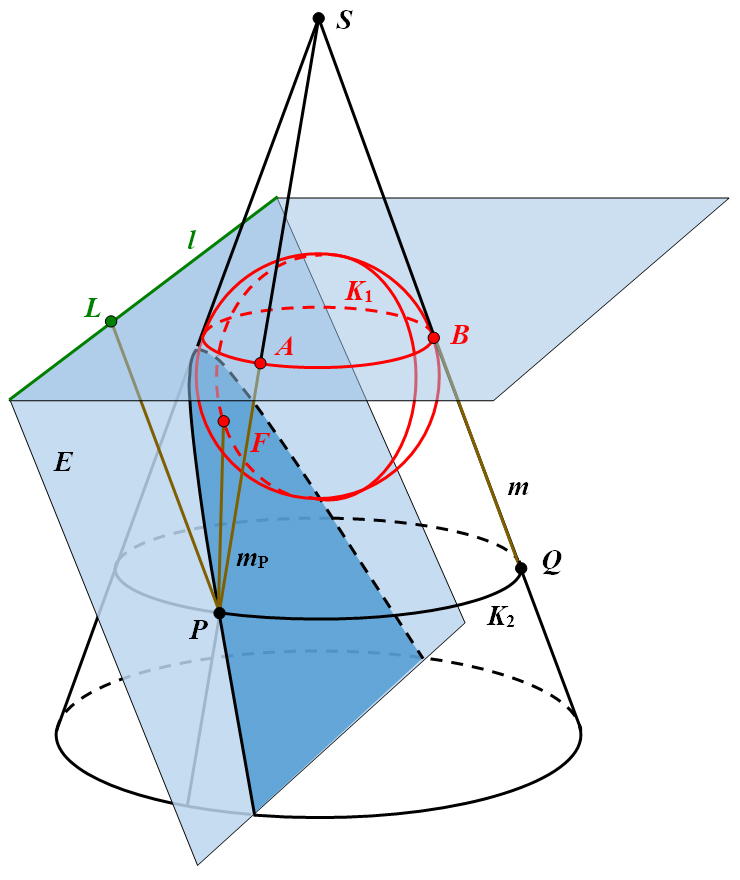
Die Mantellinie $m$ werde derart parallel im Raum verschoben, dass $Q$ auf $P$ abgebildet wird und damit das Bild der Mantellinie durch $P$ verläuft. Aufgrund der vorausgesetzten Parallelität der Schnittebene $E$ und der Mantellinie $m$ schneidet das Bild der verschobenen Mantellinie die Schnittgerade $l$ in einem Punkt $L$ (Abbildung 30).

Abbildung 30: Parabel als Kegelschnitt.

Wegen der Orthogonalität der Geraden $l$ und $m$ entspricht die Strecke $\stackrel{\_}{PL}$ dem Abstand des Punktes $P$ von der Geraden $l$. Zudem wird wegen der Parallelität der beiden Kreisebenen $K_1$ und $K_1$ ersichtlich, dass die beiden Strecken $\stackrel{\_}{QB}$ und $\stackrel{\_}{PL}$ gleichlang sind: $\left|\stackrel{\_}{QB}\right|=\left|\stackrel{\_}{PL}\right|$.

Die Parallelität der beiden Kreisebenen $K_1$ und $K_2$ und ihre Lage senkrecht zur Kegelachse führt dazu, dass die entsprechenden Abschnitte der Mantellinien $m$ und $m_P$ des geraden Kreiskegels, die Strecken $\stackrel{\_}{PA}$ und $\stackrel{\_}{QB}$, gleichlang sind: $\left|\stackrel{\_}{PA}\right|=\left|\stackrel{\_}{QB}\right|$.

Damit folgt aber wegen der Beziehungen $\left|\stackrel{\_}{PA}\right|=\left|\stackrel{\_}{PF}\right|$ und $\left|\stackrel{\_}{QB}\right|=\left|\stackrel{\_}{PL}\right|$ weiter, dass für jeden Punkt $P$ auch die Gleichung $\left|\stackrel{\_}{PF}\right|=\left|\stackrel{\_}{PL}\right|$ gilt.

Die Einbeschreibung der Dandelinschen Kugel und damit die Festlegung des Punktes $F$ und der Geraden $l$ ist unveränderlich und unabhängig von der Wahl des allgemeinen Punktes $P$ der Schnittfigur. Somit folgt aus den Betrachtungen für alle Punkte der Schnittfigur folgender Zusammenhang:

Jeder Punkt $P$ der ebenen Schnittfigur ist gleichweit von einem festen Punkt $F$ (Brennpunkt) und von einer festen Gerade $l$ (Leitlinie) entfernt. Damit ist der mittels einer zu einer Mantellinie parallelen Ebene gewonnene Kegelschnitt eine Parabel.