Die Kissoide des Diokles

Die nach ihrem Aussehen als Efeulinie (κισσος) bezeichnete ebene Kurve dritter Ordnung wird auf auf den antiken Mathematiker Diokles (vermutlich 2. Jahrhundert v. Chr.) zurückgeführt. Diokles löste mit Hilfe der Kissoide das Delische Problem der Würfelverdopplung. ([Wieleitner, S. 42] und [Van der Waerden, S. 442 ff.])

Geometrische Konstruktion

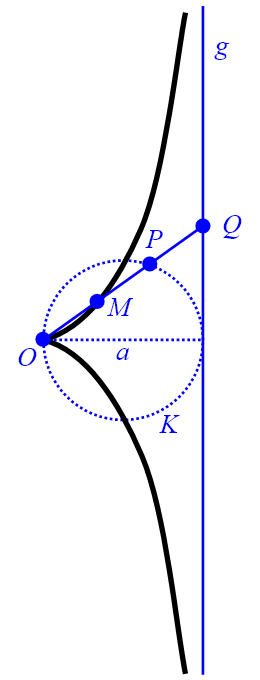
Gegeben sei ein Punkt $O$, durch den ein Kreis $K$ mit einem Durchmesser der Länge $a$ verläuft. An den von $O$ ausgehenden Kreisdurchmesser wird in den zweiten Endpunkt eine Tangente $g$ an den Kreis $K$ gelegt. Der Punkt $O$ wird als Pol, der Kreis $K$ wird als Leitkreis und die Gerade $g$ wird als Leitlinie der Kissoide bezeichnet (Abbildung 3, links).

Vom Pol $O$ aus wird eine Gerade gezeichnet, die den Leitkreis $K$ im Punkt $P$ und die Leitgerade im Punkt $Q$ schneidet. Von $Q$ aus wird auf dieser Geraden in Richtung des Pols der Punkt $M$ so abgetragen, dass $\left|\stackrel{\_}{QM}\right|=\left|\stackrel{\_}{OP}\right|$ gilt. Die Kissoide ergibt sich als geometrischer Ort aller Punkte $M$.

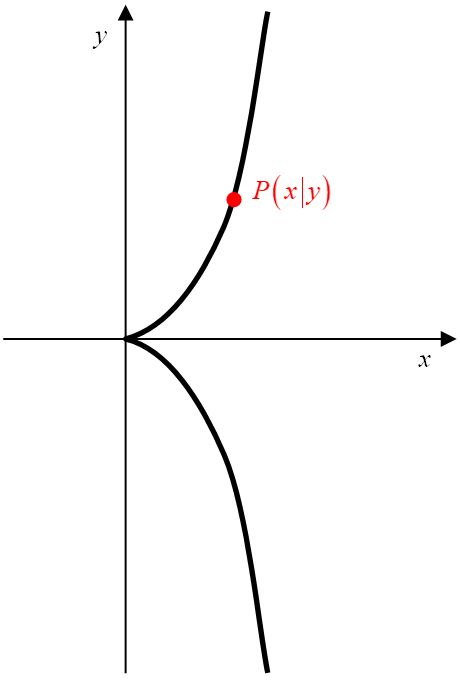
Abbildung 3: Kissiode mit Leitkreis und Leitgerade (links) und im Koordinatensystem (rechts).

Kurvengleichung und Besonderheiten

Die analytische Beschreibung der Kissoide mit Hilfe kartesischer Koordinaten erfolgt durch eine Gleichung dritten Grades. Die Kurve ergibt sich als Menge aller Punkte $P\left(x|y\right)$ der Ebene, deren Koordinaten die Gleichung erfüllen.

Kissoide des Diokles:

${\displaystyle \left(2a-x\right)y^2=x^3}$

Der Pol der Kissoide liegt im Ursprung des kartesischen Koordinatensystems. Der Punkt $\left(0|0\right)$ ist als Spitze ein singulärer Punkt der Kurve (Abbildung 3, rechts).