Die Konchoide des Nikomedes

Die wegen der Ähnlichkeit des rechten Kurvenastes zu einer Muschel (κογχη) als Konchoide oder auch Kochloide bezeichnete zweiteilige Kurve vierter Ordnung wurde von dem antiken Geometer Nikomedes (etwa 200 v. Chr.) gefunden. Nikomedes entwickelte eine mechanische Vorrichtung, um diese Kurve zu zeichnen, und löste mit Hilfe der Konchoide die klassischen Probleme der Würfelverdopplung und der Dreiteilung des Winkels. ([Wieleitner, S. 66 f.] und [Van der Waerden, S. 390 ff.])

Geometrische Konstruktion

Ausgehend von einem Punkt $O$ und einer Gerade $g$, die sich im Abstand $a$ vom Punkt $O$ befindet, werden mit Hilfe einer gegebenen Länge $l$ die Punkte der Konchoide in der Ebene konstruiert. Der Punkt $O$ wird auch als Pol und die Gerade $g$ wird auch als Leitlinie der Konchoide bezeichnet.

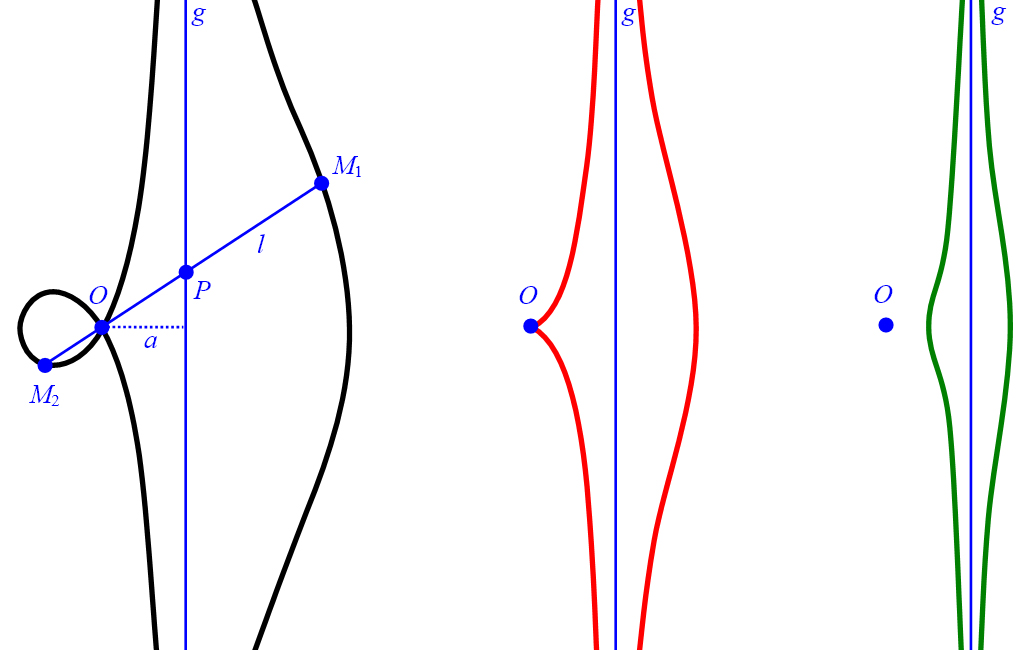
Vom Pol $O$ wird eine Gerade gezeichnet, die die Leitlinie im Punkt $P$ schneidet. Von $P$ aus werden auf dieser Gerade die beiden Punkte $M_1$ und $M_2$ abgetragen mit $\left|\stackrel{\_}{P{M}_1}\right|=\left|\stackrel{\_}{P{M}_2}\right|=l$. Die Konchoide ergibt sich als geometrischer Ort aller Punkte $M_1$ und $M_2$ (Abbildung 5, links).

Eine Konchoide besteht aufgrund der Konstruktionsvorschrift aus zwei nicht verbundenen Ästen: einem äußeren Ast hinter der Leitlinie vom Pol aus gesehen (hier die Menge der Punkte $M_1$) und einem inneren Ast auf der Polseite bezüglich der Leitlinie (hier die Menge der Punkte $M_2$). Das Verhältnis der beiden Längen ${\displaystyle \frac{l}{a}}$ bestimmt unterschiedlichen Formen der Konchoide (Abbildung 5, links, Mitte, rechts).

Abbildung 5: Konchoide mit ${\displaystyle \frac{l}{a}>1}$ (links), ${\displaystyle \frac{l}{a}=1}$ (Mitte) und ${\displaystyle \frac{l}{a}<1}$ (rechts).

Kurvengleichung und Besonderheiten

Die analytische Beschreibung der Konchoide in einem kartesischen Koordinatensystem erfolgt durch eine Gleichung vierten Grades. Die Kurve ergibt sich als Menge aller Punkte der Ebene, deren Koordinaten $\left(x|y\right)$ die Gleichung erfüllen.

Konchoide des Nikomedes:

${\displaystyle {\left(x-a\right)}^2\left(x^2+y^2\right)=l^2{x}^2}$

Der Pol der Konchoide liegt im Ursprung des kartesischen Koordinatensystems. Die beiden Längen $a$ und $l$ führen als Kurvenparameter in der Gleichung zu den unterschiedlichen Ausprägungen der Kurve.

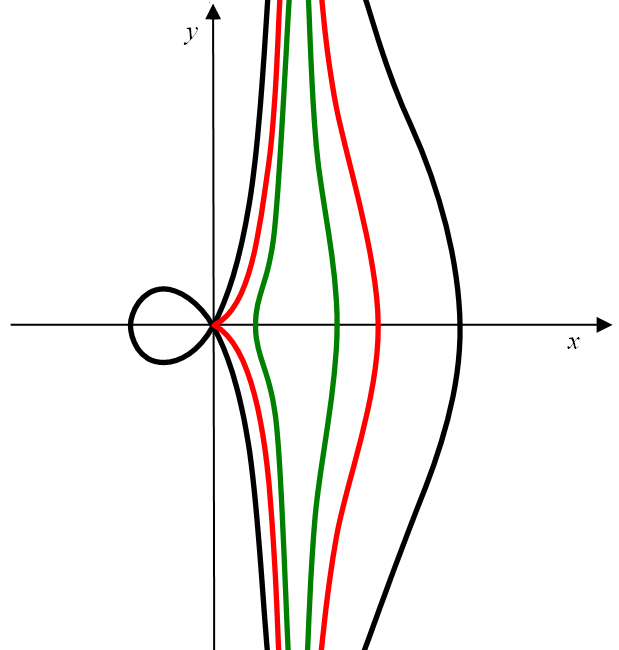
Für ${\displaystyle \frac{l}{a}>1}$ weist der innere Ast der Konchoide eine Schleife auf (Abbildung 6, schwarz). Im Pol (im Koordinatenursprung) liegt ein Doppelpunkt, d.h. der Punkt $\left(0|0\right)$ ist ein singulärer Punkt der Kurve.

Für ${\displaystyle \frac{l}{a}=1}$ wird die Schleife des innere Astes in Form einer Spitze auf den Pol zusammengezogen (Abbildung 6, rot). Der Punkt $\left(0|0\right)$ ist somit ein singulärer Punkt der Kurve.

Für ${\displaystyle \frac{l}{a}<1}$ verläuft der innere Ast der Konchoide nicht durch den Pol (Abbildung 6, grün). Allerdings gehört der Punkt $\left(0|0\right)$ dennoch zur Kurve und stellt daher als isolierter Punkt der Konchoide einen singulären Punkt der Kurve dar.

Abbildung 6: Konchoide mit ${\displaystyle \frac{l}{a}>1}$ (schwarz), ${\displaystyle \frac{l}{a}=1}$ (rot) und ${\displaystyle \frac{l}{a}<1}$ (grün) im Koordinatensystem.