Die Pascalsche Schnecke

Erstmals konstruierte Albrecht Dürer (1471-1528) die heute als Pascalsche Schnecke bekannte ebene geschlossene Kurve und nannte sie Spinnenlinie [Dürer, Abbildung 40]. Bezeichnet wird diese Kurve vierter Ordnung nach dem französischen Mathematiker Étienne Pascal (1588-1651) [Cantor 1892, S. 806]. Es gibt je nach Größe der Kurvenparameter verschiedene Ausprägungen der Pascalschen Schnecke. Ein Sonderfall liegt mit der Kardioide (Herzkurve) vor.

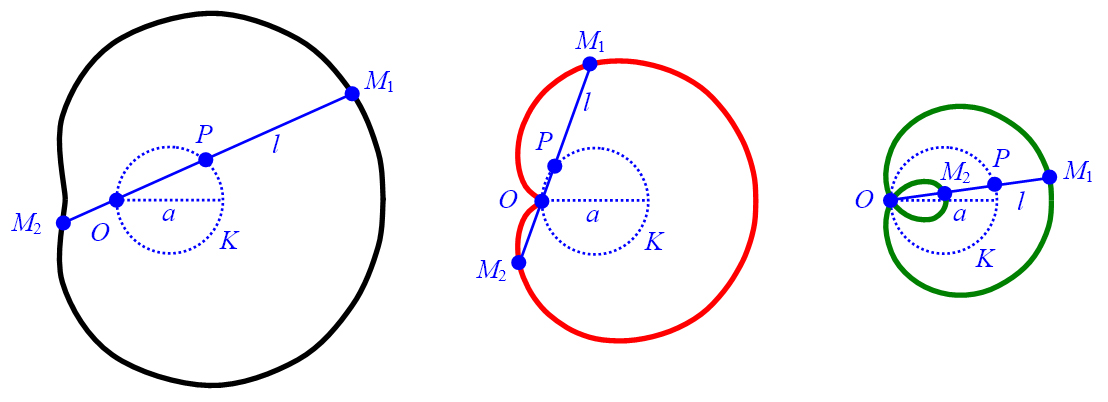
Geometrische Konstruktion

Die Konstruktion einer Pascalschen Schnecke basiert auf einem gegebenen Leitkreis $K$ mit dem Durchmesser $a$, der durch einen Punkt $O$ (auch als Pol bezeichnet) verläuft, sowie einer gegebenen Länge $l$ (Abbildung 7).

Vom Punkt $O$ aus wird eine Gerade gezeichnet, die den Leitkreis $K$ im Punkt $P$ schneidet. Von $P$ aus werden auf der Gerade die beiden Punkte $M_1$ und $M_2$ abgetragen mit $\left|\stackrel{\_}{P{M}_1}\right|=\left|\stackrel{\_}{P{M}_2}\right|=l$. Die Kurve ergibt sich als geometrischer Ort aller Punkte $M_1$ und $M_2$.

Das Verhältnis der beiden Längen ${\displaystyle \frac{l}{a}}$ führt zu unterschiedlichen Formen der Pascalschen Schnecke (Abbildung 7).

Abbildung 7: Pascalsche Schnecke mit ${\displaystyle \frac{l}{a}>1}$ (links), ${\displaystyle \frac{l}{a}=1}$ (Mitte) und ${\displaystyle \frac{l}{a}<1}$ (rechts).

Kurvengleichung und Besonderheiten

Die analytische Beschreibung der Pascalschen Schnecke mit Hilfe kartesischer Koordinaten erfolgt durch eine Gleichung vierten Grades. Die Kurve ergibt sich als Menge aller Punkte der Ebene, deren Koordinaten $\left(x|y\right)$ die Gleichung erfüllen.

Pascalsche Schnecke:

${\displaystyle {\left(x^2+y^2-a{x}^2\right)}^2=l^2\left(x^2+y^2\right)}$

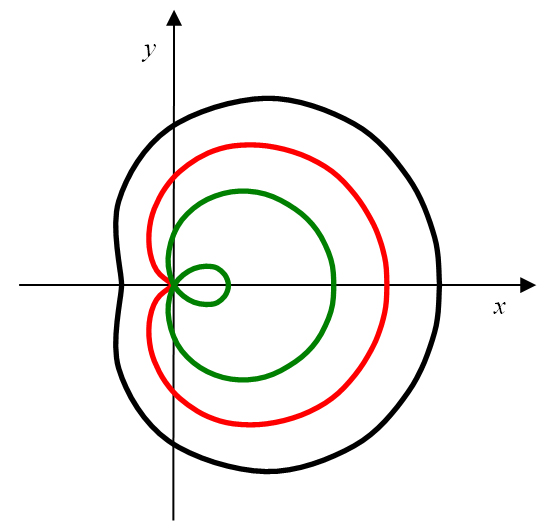
Der Pol der Pascalschen Schnecke liegt im Ursprung des kartesischen Koordinatensystems. Die beiden Längen $a$ und $l$ führen als Kurvenparameter in der Gleichung zu den unterschiedlichen Ausprägungen der Kurve.

Für ${\displaystyle \frac{l}{a}>1}$ ist die Pascalsche Schnecke eine geschlossene Kurve ohne Selbstüberschneidung (Abbildung 8, schwarz).

Für ${\displaystyle \frac{l}{a}<1}$ schneidet sich die Pascalsche Schnecke selbst im Pol und bildet einen inneren Kurvenzweig und einen äußeren Kurvenzweig aus (Abbildung 8, grün). Der Punkt $\left(0|0\right)$ ist als Doppelpunkt ein singulärer Punkt der Kurve.

Für ${\displaystyle \frac{l}{a}=1}$ wird der innere Zweig auf den Pol zusammengezogen, es entsteht die Kardioide (Abbildung 8, rot). Der Punkt $\left(0|0\right)$ ist als Spitze ein singulärer Punkt der Kurve.

Abbildung 8: Pascalsche Schnecke mit ${\displaystyle \frac{l}{a}>1}$ (schwarz), ${\displaystyle \frac{l}{a}=1}$ (rot) und ${\displaystyle \frac{l}{a}<1}$ (grün) im Koordinatensystem.