Die Strophoide

Die als Strophoide bezeichnete ebene Kurve dritter Ordnung geht vermutlich auf Gilles Personne de Roberval (1602-1675) zurück und wurde erstmals in der Literatur von Evangelista Torricelli (1608-1647) beschrieben. Den Namen der Kurve prägte Enrico Montucci (1808-1877), der 1846 die Gestalt und insbesondere die Wendung und Drehung der Kurvenlinie (στροφος) charakterisierte [Loria 1902, S. 59 ff.].

Geometrische Konstruktion

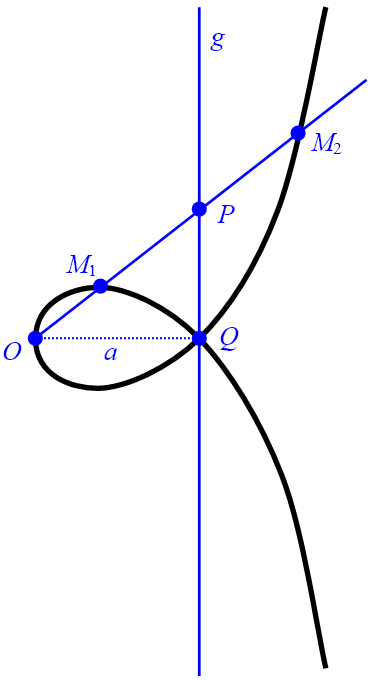
Ausgehend von einem Punkt $O$ wird in einem Abstand der Länge $a$ eine Gerade $g$ senkrecht zur Abstandslinie errichtet. Der Endpunkt der Abstandslinie sei der Punkt $Q$. Der Punkt $O$ wird als Pol und die Gerade $g$ wird als Leitlinie der Strophoide bezeichnet (Abbildung 4, links).

Vom Pol $O$ aus wird eine Gerade gezeichnet, die die Leitlinie $g$ im Punkt $P$ schneidet. Von $P$ aus werden mit der Länge $\left|\stackrel{\_}{PQ}\right|$ auf dieser Geraden die beiden Punkte $M_1$ und $M_2$ derart abgetragen, dass gilt $\left|\stackrel{\_}{P{M}_1}\right|=\left|\stackrel{\_}{P{M}_2}\right|=\left|\stackrel{\_}{PQ}\right|$. Die Strophoide ergibt sich als geometrischer Ort aller Punkte $M_1$ und $M_2$.

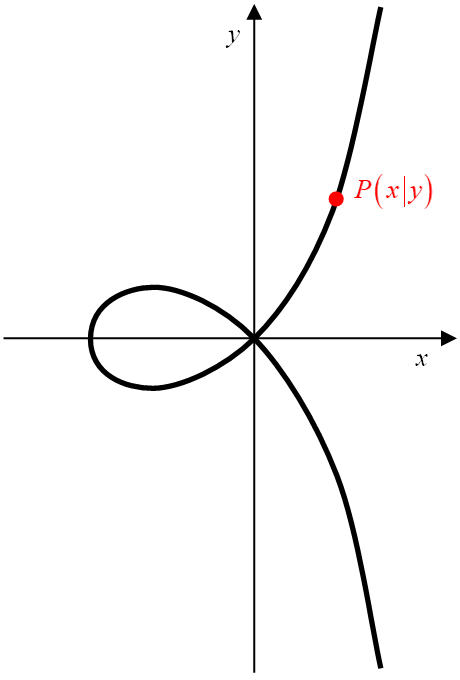
Abbildung 4: Strophoide als geometrische Figur (links) und im Koordinatensystem (rechts).

Kurvengleichung und Besonderheiten

Die analytische Beschreibung der Strophoide in einem kartesischen Koordinatensystem erfolgt durch eine Gleichung dritten Grades. Die Kurve ergibt sich als Menge aller Punkte $P\left(x|y\right)$ der Ebene, deren Koordinaten die Gleichung erfüllen.

Strophoide:

${\displaystyle \left(a-x\right)y^2=\left(a+x\right)x^2}$

In der Darstellung im Koordinatensystem (Abbildung 4, rechts) entsteht eine nicht geschlossene Kurve, bestehend aus einer Schleife und zwei unendlichen Zweigen. Im Punkt ${\displaystyle \left(0|0\right)}$, im Koordinatenursprung, liegt ein Doppelpunkt als ein singulärer Punkt der Strophoide.