Geometrische Definition einer Ellipse mit Brennpunkten

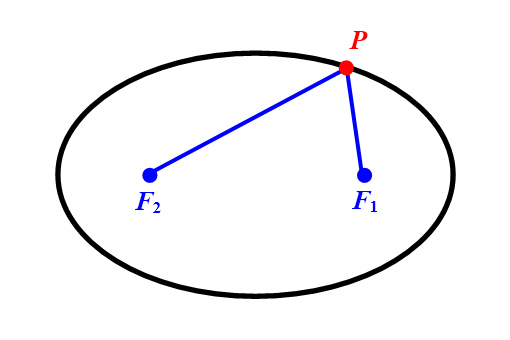
Eine Ellipse ist die Menge aller Punkte $P$ einer Ebene, für die die Summe der Abstände von zwei gegebenen festen Punkten (Brennpunkten) $F_1$ und $F_2$ konstant ist: $\left|\stackrel{\_}{P{F}_1}\right|+\left|\stackrel{\_}{P{F}_2}\right|=2a$ (Abbildung 4).

Abbildung 4: Ellipse mit Brennpunkten.

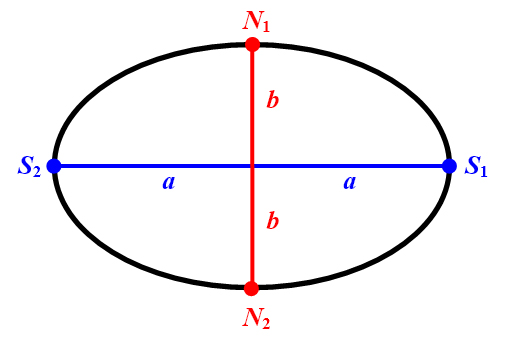
In einer Ellipse sind zwei Punkte als Scheitelpunkte $S_1$, $S_2$ sowie zwei Punkte als Nebenscheitelpunkte $N_1$, $N_2$ ausgezeichnet (Abbildung 5, links). Die Strecke zwischen den Scheitelpunkten heißt große Achse der Ellipse, ihre Länge beträgt $\left|\stackrel{\_}{S_1{S}_2}\right|=2a$. Die beiden Brennpunkte $F_1$, $F_2$ liegen auf der großen Achse. Senkrecht zur großen Achse verläuft zwischen den Nebenscheitelpunkten die kleine Achse der Ellipse, ihre Länge beträgt $\left|\stackrel{\_}{N_1{N}_2}\right|=2b$.

Die beiden Ellipsenachsen sind orthogonal und halbieren einander. Entsprechend der Achsenbezeichnung werden die halben Achsen mit ihren Längen $a$ und $b$ auch als große bzw. kleine Halbachsen bezeichnet.

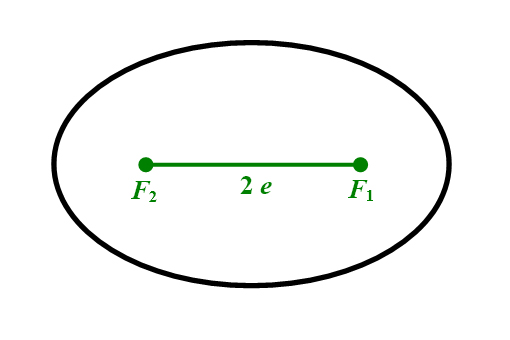
Die Verbindungslinie zwischen den beiden Brennpunkten (Abbildung 5, rechts) hat die Länge $\left|\stackrel{\_}{F_1{F}_2}\right|=2e$. Die kleine Ellipsenachse steht senkrecht auf der Verbindungslinie der beiden Brennpunkte und halbiert diese. Die Länge $e$ wird als lineare Exzentrizität bezeichnet.

Der Mittelpunkt der Verbindungslinie der beiden Scheitelpunkte, der auch Mittelpunkt der Verbindungslinie der beiden Brennpunkte ist, wird Mittelpunkt der Ellipse genannt.

Abbildung 5: Ellipse mit Achsen und Halbachsen (links) und mit linearer Exzentrizität (rechts).