Die analytische Beschreibung einer Ellipse

Aus der Brennpunkteigenschaft einer Ellipse lässt sich eine analytische Gleichung der Ellipse in der Normalform ableiten.

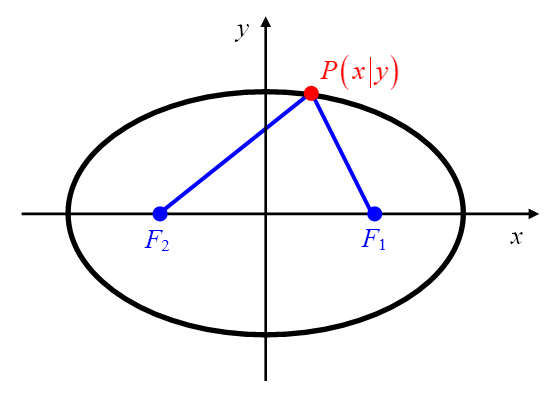
Für die Entwicklung einer Kurvengleichung, die die Ellipsenpunkte beschreibt, wird der Ellipse ein kartesisches Koordinatensystem derart einbeschrieben, dass die Abszissenachse mit der großen Ellipsenachse und die Ordinatenachse mit der kleinen Ellipsenachse zusammenfällt (Abbildung 8). Aufgrund der geometrischen Besonderheiten der Ellipse ist damit der Koordinatenursprung zugleich der Mittelpunkt der Verbindungslinie der beiden Brennpunkte $F_1\left(e|0\right)$ und $F_2\left(-e|0\right)$.

Abbildung 8: Ellipse im Koordinatensystem.

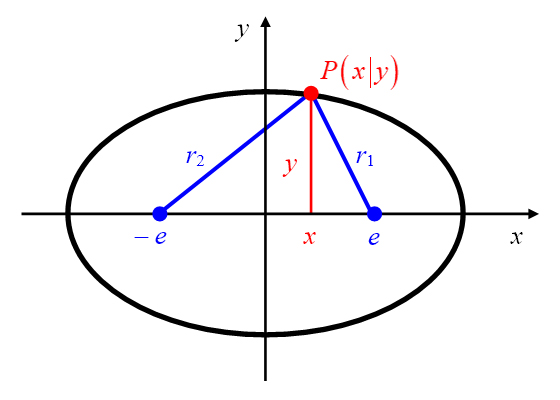
Mit Hilfe der Markierung der Abszissenlänge $x$ und der Ordinatenlänge $y$ des allgemeinen Ellipsenpunktes $P\left(x|y\right)$ lässt sich das Dreieck $F_{1}P{F}_2$ in zwei rechtwinklige Dreiecke zerlegen (Abbildung 9, links). Nach dem Satz des Pythogoras gelten für die Seitenlängen der beiden Dreiecke die Gleichungen (1) ${\left(e-x\right)}^2+y^2={r_1}^2$ und (2) ${\left(x+e\right)}^2+y^2={r_2}^2$.
Aus der Ellipseneigenschaft $\left|\stackrel{\_}{F_{1}P}\right|+\left|\stackrel{\_}{F_{2}P}\right|=2a$ folgt zudem die Gleichung $r_1+r_2=2a$.

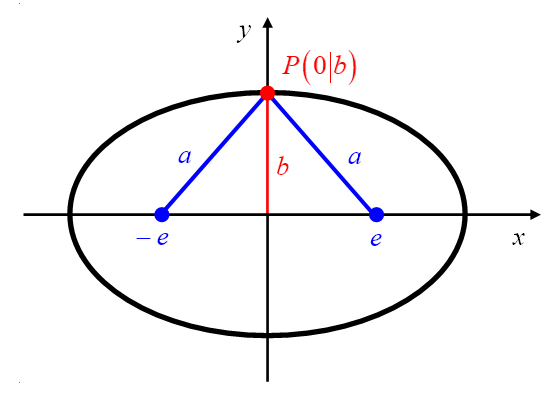
In dem speziellen Fall, dass der Ellipsenpunkt im Nebenscheitelpunkt $P\left(0|b\right)$ liegt, entstehen durch die Zerlegung zwei kongruente rechtwinklige Dreiecke (Abbildung 9, rechts). Aus der Ellipseneigenschaft und aus der Ellipsensymmetrie lässt sich somit die Beziehung (3) $e^2+b^2=a^2$ ableiten.

Abbildung 9: Ellipse mit einer Dreieckszerlegung (links) und im Spezialfall (rechts).

Aus der Gleichung $r_1+r_2=2a$ wird durch geschicktes Umformen, zweimaliges Quadrieren, Einsetzen der pythagoräischen Beziehungen (1), (2) und (3) und fortgesetztes Vereinfachen die Ellipsengleichung in der Normalform gewonnen:

$${\displaystyle \begin{array}{rcll}{r}_1+r_2& =& 2a& |-r_2\\ r_1& =& 2a-r_2& |{\left(\right)}^2\\ {r_1}^2& =& 4a^2-4a{r}_2+{r_2}^2& |-4a^2-{r_2}^2\\ {r_1}^2-{r_2}^2-4a^2& =& -4a{r}_2& |{r_1}^2\text{ , }{r_2}^2\\ {\left(e-x\right)}^2+y^2-{\left(e+x\right)}^2-y^2-4a^2& =& -4a{r}_2& \\ -4ex-4a^2& =& -4a{r}_2& |:\left(-4\right)\\ ex+a^2& =& a{r}_2& |{\left(\right)}^2\\ e^2{x}^2+2ex{a}^2+a^4& =& a^2{r_2}^2& |{r_2}^2\\ e^2{x}^2+2ex{a}^2+a^4& =& a^2{\left(e+x\right)}^2+a^2{y}^2& \\ e^2{x}^2+2ex{a}^2+a^4& =& a^2{e}^2+2ex{a}^2+a^2{x}^2+a^2{y}^2& |-2ex{a}^2\\ e^2{x}^2+a^4& =& a^2{e}^2+a^2{x}^2+a^2{y}^2& |-a^2{x}^2-a^2{y}^2-a^4\\ e^2{x}^2-a^2{x}^2-a^2{y}^2& =& a^2{e}^2-a^4& |\left(\right)\\ \left(e^2-a^2\right)x^2-a^2{y}^2& =& a^2\left(e^2-a^2\right)& |·\left(-1\right)\\ \left(a^2-e^2\right)x^2+a^2{y}^2& =& a^2\left(a^2-e^2\right)& |b^2=a^2-e^2\\ b^2{x}^2+a^2{y}^2& =& a^2{b}^2& |:a^2{b}^2\\ {\displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2}}& =& 1& \end{array}}$$

Im Ergebnis der analytischen Betrachtungen wurde aus der geometrischen Definition der Ellipse durch äquivalentes Umformen eine Kurvengleichung abgeleitet, die die Normalform der Ellipsengleichung als Kegelschnittgleichung darstellt mit Angabe der großen und kleinen Halbachsenlänge. Die Äquivalenz der geometrischen Definition der Ellipse und der analytischen Definition der Ellipse mittels Kegelschnittgleichung und mithin als Kurve zweiter Ordnung wurde somit bewiesen.