Asymptoten und Halbachsen der Hyperbel

In der Ableitung der Normalform der Hyperbelgleichung wurde ein Parameter $b$ mit $a^2+b^2=e^2$ definiert, der einen Zusammenhang zwischen der großen Halbachse $a$ und der linearen Exzentrizität $e$ herstellt. Dieser Parameter wird in Analogie zur Ellipse als imaginäre kleine Halbachse bezeichnet.

Eine geometrische Darstellung der beiden Halbachsen erwächst aus der Betrachtung der beiden Asymptoten $t_1$ und $t_1$ der Hyperbel (Abbildung 21). Die Asymptotengleichungen lassen sich hierfür ableiten aus der Hyperbelgleichung, umgestellt nach $y$.

Aus der Hyperbelgleichung ${\displaystyle \frac{x^2}{a^2}-\frac{y^2}{b^2}=1}$ entstehen zwei Gleichungen, die die funktionale Abhängigkeiten der Koordinaten der Hyperbelpunkte wiedergeben: ${\displaystyle y=b·\sqrt{\frac{x^2}{a^2}-1}}$ und ${\displaystyle y=-b·\sqrt{\frac{x^2}{a^2}-1}}$.

Für $x\ne 0$ können die Gleichungen umgeformt werden in ${\displaystyle y=\frac{b}{a}x·\sqrt{1-\frac{a^2}{x^2}}}$ und ${\displaystyle y=-\frac{b}{a}x·\sqrt{1-\frac{a^2}{x^2}}}$, so dass für betragsmäßig große $x$ die beiden Asymptotengleichungen leicht ersichtlich sind: ${\displaystyle t_1\text{:}y=\frac{b}{a}x}$ und ${\displaystyle t_2\text{:}y=-\frac{b}{a}x}$.

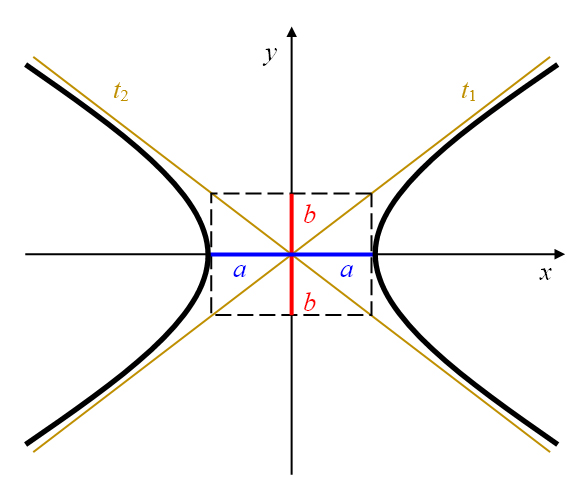
Abbildung 21: Hyperbel mit Asymptoten und beiden Halbachsen.

Die Ordinatenwerte, die aus den Abszissenwerten $a$ und $-a$ der beiden Scheitelpunkte $S_1$ und $S_2$ in den Asymptotengleichungen gebildet werden, entsprechen betragsmäßig der Länge der imaginären reellen Halbachse $b$. Diese kann somit im Koordinatensystem dargestellt werden (Abbildung 21).