Geometrische Definition einer Hyperbel mit Leitlinien

Auch für die Hyperbel gibt es eine zweite geometrische Definition, die den Abstand eines Hyperbelpunktes von einem Brennpunkt und den Abstand des Hyperbelpunktes zu einer festen Linie, der Leitlinie, betrachtet (Abbildung 17).

Eine Hyperbel ist die Menge aller Punkte $P$ einer Ebene, für die das Verhältnis des Abstandes des Punktes $P$ von einem festen Punkt (Brennpunkt) $F$ zu dem Abstand des Punktes $P$ von einer zugehörigen Leitlinie $l$ konstant und größer als $1$ ist.

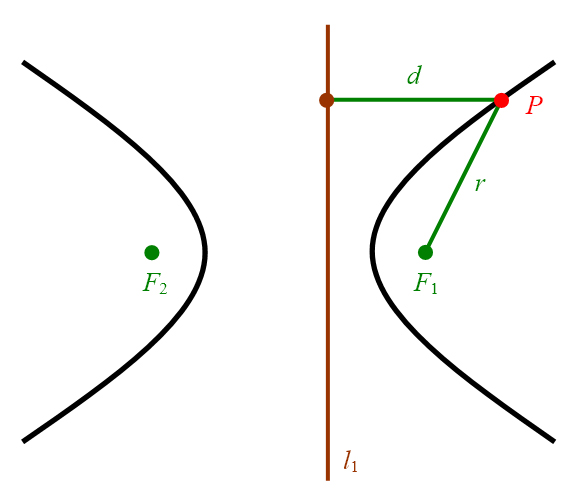
Abbildung 17: Hyperbel mit einem Brennpunkt und zugehöriger Leitlinie.

Sei $r=\left|\stackrel{\_}{P{F}_1}\right|$ und sei $d$ der Abstand des Punktes $P$ zu der Leitlinie $l_1$, dann gilt für alle Hyperbelpunkte ${\displaystyle \frac{r}{d}=\epsilon }$ mit $\epsilon >1$.

Der konstante Wert $\epsilon$ wird als numerische Exzentrizität bezeichnet. Die numerische Exzentrizität steht in einem unmittelbarem Zusammenhang zur großen Halbachsenlänge $a$ und zur linearen Exzentrizität $e$ (halber Abstand der beiden Brennpunkte): es gilt ${\displaystyle \epsilon =\frac{e}{a}}$.

Zu jedem Brennpunkt der Hyperbel $F_1$ und $F_2$ gibt es eine zugehörige Leitlinie $l_1$ und $l_2$. Die beiden Leitlinien sind orthogonal zur großen Achse der Hyperbel und im Abstand ${\displaystyle \frac{a}{\epsilon }}$ vom Mittelpunkt der Hyperbel angeordnet (Abbildung 18).

Dabei ist für jeden Hyperbelpunkt das Verhältnis der jeweiligen Abstände ${\displaystyle \frac{r_1}{d_1}}$ und ${\displaystyle \frac{r_2}{d_2}}$ gleich und konstant: ${\displaystyle \frac{r_1}{d_1}=\frac{r_2}{d_2}=\epsilon }$.

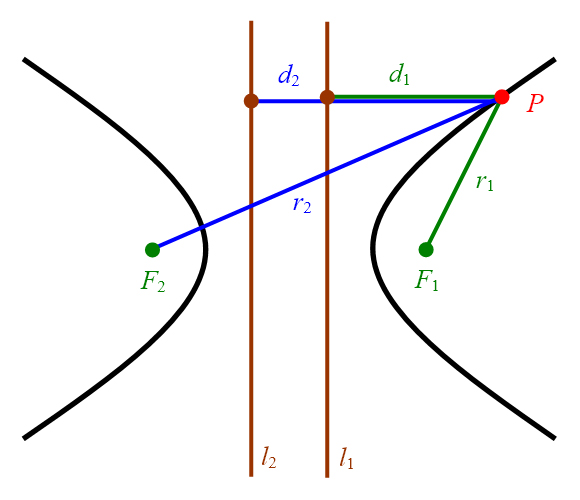
Abbildung 18: Hyperbel mit Brennpunkten und Leitlinien.

Aus der Leitlinieneigenschaft der Hyperbel ${\displaystyle \frac{r_1}{d_1}=\frac{r_2}{d_2}=\epsilon }$ folgt $r_1=\epsilon ·d_1$ und $r_2=\epsilon ·d_2$.

Der Abstand der Leitlinie vom Mittelpunkt der Hyperbel beträgt ${\displaystyle \frac{a}{\epsilon }}$, somit liegen beide Leitlinien im konstanten Abstand ${\displaystyle 2·\frac{a}{\epsilon }}$ voneinander entfernt.

Weiterhin lässt sich der konstante Abstand der beiden Leitlinien als Betrag der Differenz der Längen $d_1$ und $d_2$ formulieren (gut ersichtlich in Abbildung 18). Es gilt für den rechten Hyperbelast ${\displaystyle d_2-d_1=2·\frac{a}{\epsilon }}$ (analog $d_1-d_2$ für den linken Hyperbelast).

Für die Differenz der Brennpunktabstände eines Punktes des rechten Hyperbelastes (linker Hyperbelast analog) ergibt sich dann:

$${\displaystyle \begin{array}{rcl}{r}_2-$ r_1$& =& \epsilon ·d_2-\epsilon ·d_1\\ r_2-$ r_1$& =& \epsilon \left(d_2-d_1\right)\\ r_2-$ r_1$& =& \epsilon \left(2·\frac{a}{\epsilon }\right)\\ r_2-$ r_1$& =& 2a\end{array}}$$

Damit folgt aus der Leitlinieneigenschaft die Brennpunkteigenschaft der Hyperbel.