Die analytische Beschreibung einer Hyperbel

Aus der Brennpunkteigenschaft einer Hyperbel lässt sich eine analytische Gleichung der Hyperbel in der Normalform ableiten.

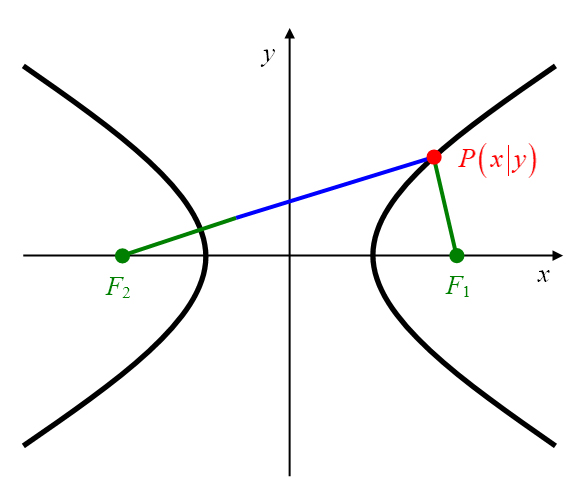
Hierfür wird der Hyperbel ein kartesisches Koordinatensystem derart einbeschrieben, dass der Koordinatenursprung in den Mittelpunkt der Verbindungslinie der beiden Brennpunkte $F_1\left(e|0\right)$ und $F_2\left(-e|0\right)$ (den Mittelpunkt der Hyperbel) gelegt wird und die die Abszissenachse mit der großen Hyperbelachse zusammenfällt (Abbildung 19).

Abbildung 19: Hyperbel im Koordinatensystem.

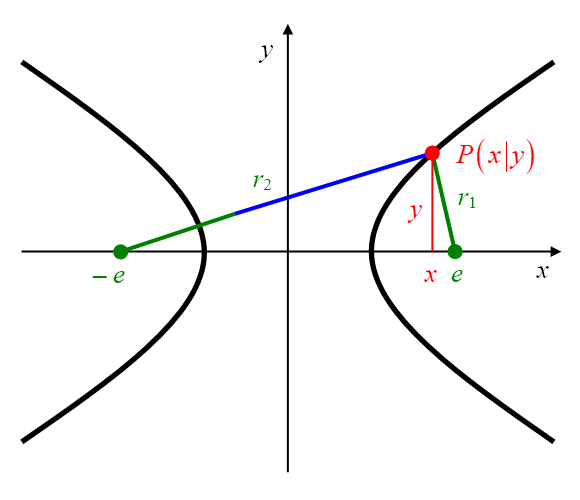
Mit Hilfe der Markierung der Abszissenlänge $x$ und der Ordinatenlänge $y$ des allgemeinen Hyperbelpunktes $P\left(x|y\right)$ lässt sich das Dreieck $F_{1}P{F}_2$ in zwei rechtwinklige Dreiecke zerlegen (Abbildung 20). Nach dem Satz des Pythogoras gelten für die Seitenlängen der beiden Dreiecke die Gleichungen (1) ${\left(e-x\right)}^2+y^2={r_1}^2$ und (2) ${\left(x+e\right)}^2+y^2={r_2}^2$.

Aufgrund der geometrischen Besonderheiten der Hyperbel gilt stets $e>a$. Es wird ein Paramter $b$ definiert, so dass $a^2+b^2=e^2$ gilt und mithin die Beziehung (3) $b^2=e^2-a^2$ folgt.

Aus der Hyperbeleigenschaft $\left|\left|\stackrel{\_}{F_{1}P}\right|-\left|\stackrel{\_}{F_{2}P}\right|\right|=2a$ folgt zudem die Gleichung für die Hyperbelpunkte des rechten Hyperbelastes $r_2-r_1=2a$ bzw. für die Hyperbelpunkte des linken Hyperbelastes $r_1-r_2=2a$.

Abbildung 20: Hyperbel mit einer Dreieckszerlegung.

Für den rechten Hyperbelast lässt sich aus der Gleichung $r_2-r_1=2a$ durch geschicktes Umformen, zweimaliges Quadrieren, Einsetzen der pythagoräischen Beziehungen (1), (2) und (3) und fortgesetztes Vereinfachen die Hyperbelgleichung in der Normalform ableiten (für den linken Hyperbelast erfolgt dies in analoger Weise):

$${\displaystyle \begin{array}{rcll}{r}_2-r_1& =& 2a& |+r_1\\ r_2& =& 2a+r_1& |{\left(\right)}^2\\ {r_2}^2& =& 4a^2+4a{r}_1+{r_1}^2& |-4a^2-{r_1}^2\\ {r_2}^2-{r_1}^2-4a^2& =& 4a{r}_1& |{r_1}^2\text{ , }{r_2}^2\\ {\left(e+x\right)}^2+y^2-{\left(e-x\right)}^2-y^2-4a^2& =& 4a{r}_1& \\ 4ex-4a^2& =& 4a{r}_1& |:\left(4\right)\\ ex-a^2& =& a{r}_1& |{\left(\right)}^2\\ e^2{x}^2-2ex{a}^2+a^4& =& a^2{r_1}^2& |{r_1}^2\\ e^2{x}^2-2ex{a}^2+a^4& =& a^2{\left(e-x\right)}^2+a^2{y}^2& \\ e^2{x}^2-2ex{a}^2+a^4& =& a^2{e}^2-2ex{a}^2+a^2{x}^2+a^2{y}^2& |+2ex{a}^2\\ e^2{x}^2+a^4& =& a^2{e}^2+a^2{x}^2+a^2{y}^2& |-a^2{x}^2-a^2{y}^2-a^4\\ e^2{x}^2-a^2{x}^2-a^2{y}^2& =& a^2{e}^2-a^4& |\left(\right)\\ \left(e^2-a^2\right)x^2-a^2{y}^2& =& a^2\left(e^2-a^2\right)& |b^2=e^2-a^2\\ b^2{x}^2-a^2{y}^2& =& a^2{b}^2& |:a^2{b}^2\\ {\displaystyle \frac{x^2}{a^2}-\frac{y^2}{b^2}}& =& 1& \end{array}}$$

Im Ergebnis der analytischen Betrachtungen wurde aus der geometrischen Definition der Hyperbel durch äquivalentes Umformen eine Kurvengleichung abgeleitet, die die Normalform der Hyperbelgleichung als Kegelschnittgleichung darstellt. Die Äquivalenz der geometrischen Definition der Hyperbel und der analytischen Definition der Hyperbel mittels Kegelschnittgleichung und mithin als Kurve zweiter Ordnung wurde somit bewiesen.