Die Hyperbel als Kegelschnitt

Eine Hyperbel wird geometrisch als Punktmenge der Ebene definiert, für deren Punkte die Differenz der Abstände von zwei Brennpunkten einen konstanten Betrag hat. Zu untersuchen ist, ob die ebene Schnittfigur, die beim Schnitt einer Ebene mit einem geraden Doppelkegel entsteht, ebenfalls eine Hyperbel ist. Dazu werden in den Doppelkegel auf eine bestimmte Art und Weise zwei Dandelinsche Kugenl (benannt nach Germinal Pierre Dandelin, 1794-1847) einbeschrieben und es wird mit Hilfe der Kugeln gezeigt, dass für alle Punkte der Schnittfigur die Brennpunkteigenschaft der Hyperbel gilt.

Ein gerader Doppelkegel werde derart von einer Ebene geschnitten, dass diese die Kegelspitze nicht enthält, dass die Ebene nicht senkrecht zur Kegelachse und nicht parallel zu einer Mantellinie des Kegels verläuft und dass Mantellinien auf beiden Seiten der Kegelspitze geschnitten werden. Es entsteht eine ebene Schnittfigur, bestehend aus zwei Ästen.

In den Doppelkegel werden zwei Kugeln mit dem Mittelpunkt auf der Kegelachse, bezeichnet als Dandelinsche Kugeln, einbeschrieben. Die erste Kugel wird unterhalb der Kegelspitze $S$ so festgelegt, dass sie die Schnittebene in genau einem Punkt $F_1$ und den Kegel auf einer Kreislinie $K_1$ berührt. Aufgrund der Symmetrie des geraden Kegels und der Kugel liegt die Kreisebene des horizontalen Berührungskreises senkrecht zur Kegelachse. Die zweite Kugel wird oberhalb der Kegelspitze $S$ so in den Kegel einbeschrieben, dass auch sie die Schnittebene in genau einem Punkt $F_2$ und den Kegel auf einer Kreislinie $K_2$ berührt. Auch hier liegt die Kreisebene des horizontalen Berührungskreises senkrecht zur Kegelachse. 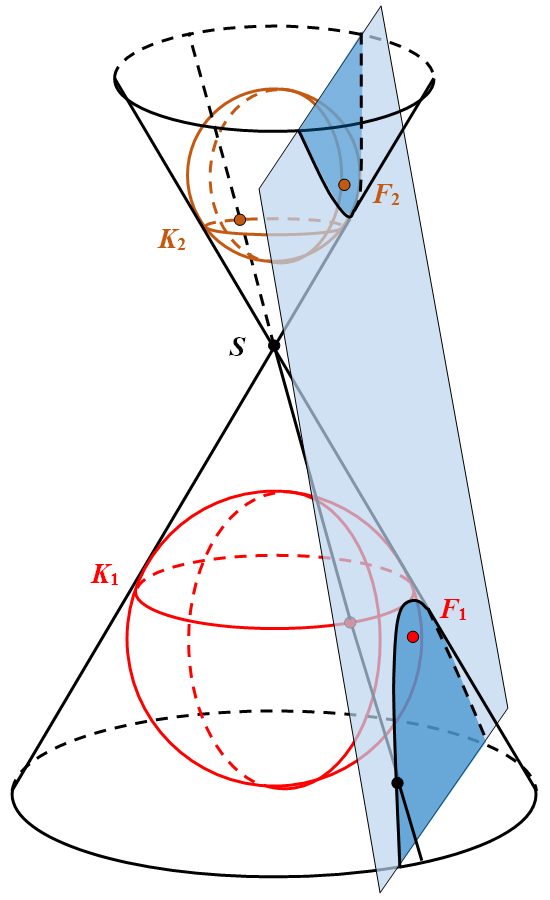Da die Schnittebene die Kegelspitze nicht enthält, existieren beide Kugeln und sind in ihrem Radius und ihrer Lage eindeutig (Abbildung 22).

Abbildung 22: Dandelinsche Kugeln am Doppelkegel.

Es sei $P$ ein allgemeiner Punkt der Schnittfigur. Ohne Beschränkung der Allgemeinheit soll der Punkt $P$ auf dem unteren Ast der Schnittfigur liegen. Der Punkt $P$ liegt auf einer Mantellinie des geraden Kreiskegels. Auf dieser Mantellinie liegen auch ein Berührungspunkt $A$ des Kreises $K_1$, die Kegelspitze $S$ und ein Berührungspunkt $B$ des Kreises $K_2$ (Abbildung 23).

In der genaueren Betrachtung der Strecken $\stackrel{\_}{P{F}_1}$ und $\stackrel{\_}{PA}$ wird offensichtlich, dass diese Strecken Tangentenabschnitte über derselben Kugel und vom selben Punkt ausgehend sind, es gilt somit für jeden Punkt $P$ der Schnittfigur $\left|\stackrel{\_}{P{F}_1}\right|=\left|\stackrel{\_}{PA}\right|$.

Gleicherart sind sind die Strecken $\stackrel{\_}{P{F}_2}$ und der Abschnitt der Mantellinie $\stackrel{\_}{PB}$ Tangentenabschnitte über derselben Kugel und vom selben Punkt ausgehend. Auch hier gilt somit für jeden Punkt $P$ der Schnittfigur $\left|\stackrel{\_}{P{F}_2}\right|=\left|\stackrel{\_}{PB}\right|$.

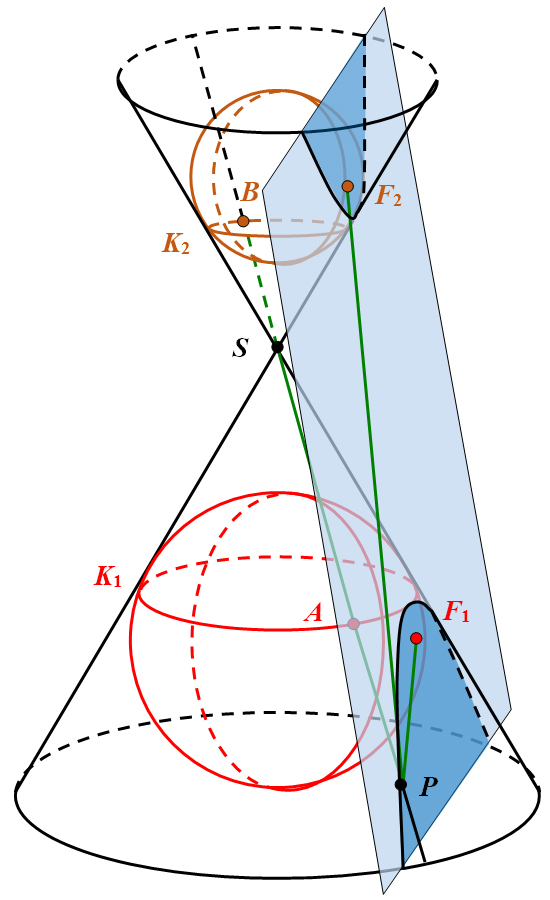
Abbildung 23: Hyperbel als Kegelschnitt.

Die Parallelität der beiden Kreisebenen $K_1$ und $K_2$ wegen ihrer Lage senkrecht zur Kegelachse führt dazu, dass die entsprechenden Abschnitte der Mantellinie des geraden Kreiskegels, die Strecken $\stackrel{\_}{AB}$, für jeden Punkt $P$ der Schnittfigur gleichlang sind. Diese konstante Länge kann als $2a$ definiert werden. Es gilt also $\left|\stackrel{\_}{AB}\right|=2a$ für jeden Punkt $P$.

Aufgrund der Festlegung der Dandelinschen Kugeln und der Lage von $P$, $A$ und $B$ auf der gleichen Mantellinie gilt auch für jeden Punkt $P$ der Schnittfigur: $\left|\stackrel{\_}{PA}\right|+\left|\stackrel{\_}{AB}\right|=\left|\stackrel{\_}{PB}\right|$.

Mit den oben betrachteten Tangentenabschnitten und den Beziehungen $\left|\stackrel{\_}{P{F}_1}\right|=\left|\stackrel{\_}{PA}\right|$ und $\left|\stackrel{\_}{P{F}_2}\right|=\left|\stackrel{\_}{PB}\right|$ folgt dann $\left|\stackrel{\_}{P{F}_1}\right|+\left|\stackrel{\_}{AB}\right|=\left|\stackrel{\_}{P{F}_2}\right|$ und mit $\left|\stackrel{\_}{AB}\right|=2a$ und der Umstellung nach $2a$ folgt $\left|\stackrel{\_}{P{F}_2}\right|-\left|\stackrel{\_}{P{F}_1}\right|=2a$ für jeden Punkt $P$ der Schnittfigur.

Die Einbeschreibung der Dandelinschen Kugeln und damit die Festlegung der Punkte $F_1$ und $F_2$ erfolgte unveränderlich und unabhängig von der Wahl des allgemeinen Punktes $P$ der Schnittfigur. Analog zur Betrachtung des allgemeinen Punktes im unteren Ast der Schnittfigur kann vorgegangen werden durch die Betrachtung eines Punktes im oberen Ast der Schnittfigur. Insgesamt ergibt sich:

Für jeden Punkt $P$ der Schnittfigur ist die Differenz der Abstände von zwei gegebenen festen Punkten (Brennpunkten) $F_1$ und $F_2$ im Betrag stets konstant, mithin ist der betrachtete Kegelschnitt eine Hyperbel.