| mathematik - physik - informatik |


|
| www.maphi.de |
| Mathematik |
| Flächen zweiter Ordnung |
| Analytische Beschreibung |
| Transformation in die Normalform |
| Klassifikation der Flächen |
| Elliptisches Paraboloid |
| Hyperbolisches Paraboloid |
| Ellipsoid |
| Einschaliges Hyperboloid |
| Zweischaliges Hyperboloid |
| Uneigentliche Flächen |
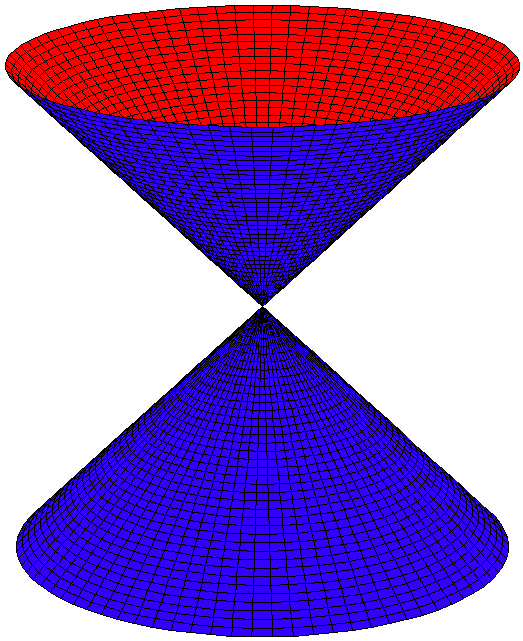
| Doppelkegel |
| Zylinder |
| Ebenenpaare |
| Literatur |
| Kegelschnitte |
| Optimierungsprobleme |
| Platon und die Mathematik |
| Spezielle Kurven |
| Physik |
| Informatik |
| Chronologie |
| Datenschutz |
|
Der elliptische Doppelkegel als uneigentliche Fläche zweiter OrdnungDie reguläre Fläche zweiter Ordnung, die von der Normalformgleichung mit , beschrieben wird, stellt die Mantelfläche eines elliptischen Doppelkegels dar (Abbildung). Mittels Division lässt sich die Gleichung des Doppelkegels umformen in eine Gleichung . Wird der Doppelkegel von Ebenen senkrecht zur -Achse geschnitten, entstehen Ellipsen als Schnittfiguren oder auch Kreise (im Fall ).
|
|
Bert Xylander
-
21. Dezember 2016
'Flächen zweiter Ordnung' |


|