Zylinder als uneigentliche Flächen zweiter Ordnung

Der parabolische Zylinder

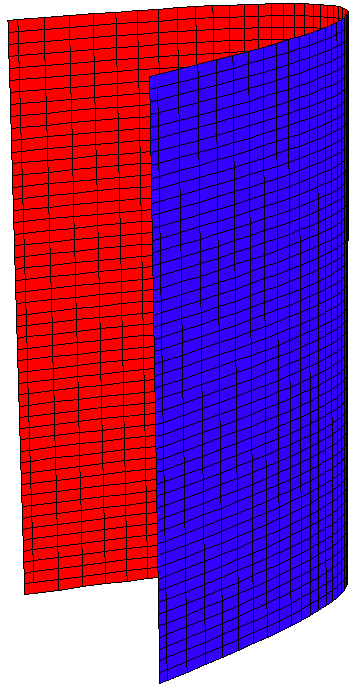
Die Mantelfläche eine parabolischen Zylinders kann mit einer Normalformgleichung einer singulären Fläche zweiter Ordnung beschrieben werden durch   $a\cdot x^2+c\cdot z=0$   mit   $a>0$, $c\ne 0$.

Üblicherweise wird diese Normalformgleichung umgewandelt in die Form   $x^2-2py=0$. Dabei sind die Koordinaten $y$ und $z$ getauscht, so dass der Zylinder senkrecht zur $x$-$y$-Ebene aufgestellt ist (Abbildung 1).

Die Schnittfiguren des parabolischen Zylinders mit Ebenen senkrecht zur $z$-Achse ergeben Parabeln, die parallel und kongruent sind zur Parabel   $x^2-2py=0$   in der $x$-$y$-Ebene.

Abbildung 1: Parabolischer Zylinder mit der Flächengleichung   $4x^2-y=0$

Der elliptische Zylinder

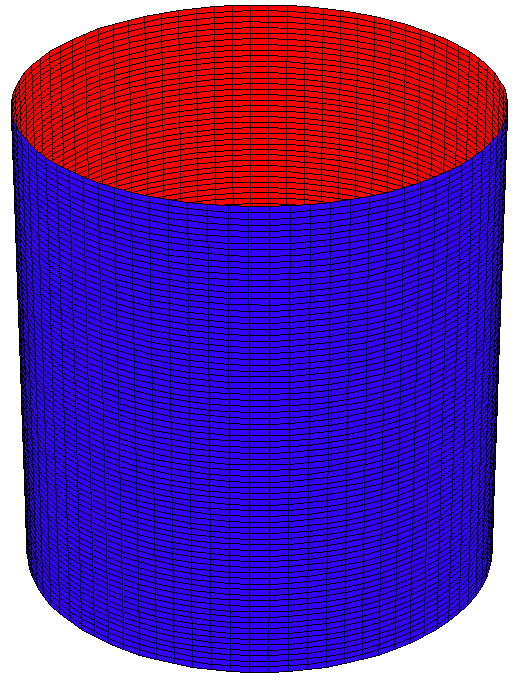
Die Normalform   $a{x}^2+b{y}^2+d=0$   mit   $a,b>0$, $d<0$   beschreibt als reguläre Fläche zweiter Ordnung die Mantelfläche eines elliptischen Zylinders (Abbildung 2).

Die Gleichung der Normalform lässt sich umformen in die Gestalt   $\frac{x^2}{p^2}+\frac{y^2}{q^2}=1$.

Die Schnittfiguren des elleptischen Zylinders mit Ebenen senkrecht zur $z$-Achse ergeben Ellipsen, die parallel und kongruent sind zur der Ellipse   $\frac{x^2}{p^2}+\frac{y^2}{q^2}=1$   in der $x$-$y$-Ebene. Für $p=q$ gehen die Ellipsen in Kreise über, es entsteht ein Kreiszylinder.

Abbildung 2: Elliptischer Zylinder mit der Flächengleichung   $3x^2+2y^2-1=0$

Der hyperbolische Zylinder

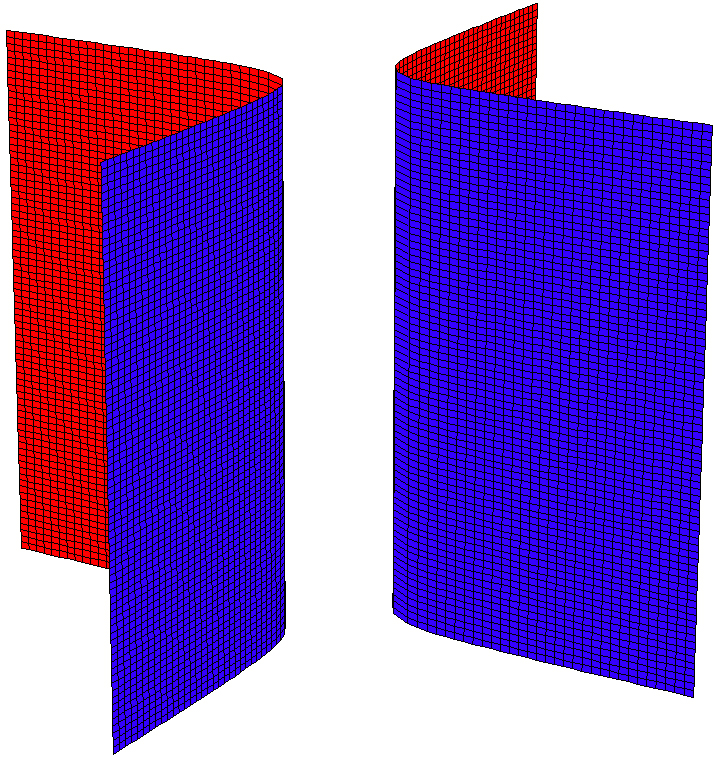
Die Mantelfläche eines hyperbolischen Zylinders lässt sich als reguläre Fläche zweiter Ordnung mit der Normalformgleichung   $a{x}^2+b{y}^2+d=0$   mit   $a>0$, $b<0$, $d\ne 0$   beschreiben. Dabei besteht die Fläche aus zwei symmetrisch zur $x$-$z$-Ebene liegenden, nichtzusammenhängenden Teilflächen (Abbildung 3).

Die Gleichung der Normalform lässt sich umformen zu   $\frac{x^2}{p^2}-\frac{y^2}{q^2}=1$.

Die Schnittfiguren des hyperbolischen Zylinders mit Ebenen senkrecht zur $z$-Achse ergeben damit Hyperbeln, die parallel und kongruent sind zur der Hyperbel   $\frac{x^2}{p^2}-\frac{y^2}{q^2}=1$   in der $x$-$y$-Ebene.

Abbildung 3: Hyperbolischer Zylinder mit der Flächengleichung   $x^2-y^2-1=0$