Ebenenpaare als uneigentliche Flächen zweiter Ordnung

Die analytische Beschreibung einer Ebene im dreidimensionalen Raum lässt sich allgemein durch eine lineare Gleichung der kartesischen Koordinaten der Ebenenpunkte erfassen in der Form   $G\cdot x+H\cdot y+I\cdot z+J=0$. Man spricht dann von einer Fläche erster Ordnung.

Dennoch können als "Entartungsfälle" aus einer Flächengleichung zweiter Ordnung eine lineare Gleichung bzw. zwei lineare Gleichungen als analytische Beschreibung einer Ebene bzw. eines Ebenenpaars entstehen. Diese Ebenen als uneigentliche Flächen zweiter Ordnung sind dabei durch speziellen Lagen im Koordinatensystem hinsichtlich der Lage zu den Koordinatenebenen ausgezeichnet.

Mit der Normalform   $a\cdot x^2+d=0$   mit   $d<0$   wird ein paralleles Ebenenpaar beschrieben (Abbildung 1).

Diese Gleichung kann mittels Division durch $d$ in eine Gleichung   $\frac{x^2}{p^2}=1$   umgeformt werden. Die beiden Ebenen liegen dann parallel zur $y$-$z$-Ebene im Abstand $x=\mathrm{\pm }p$.

Abbildung 1: Paralleles Ebenenpaar mit der Flächengleichung   $x^2-4=0$

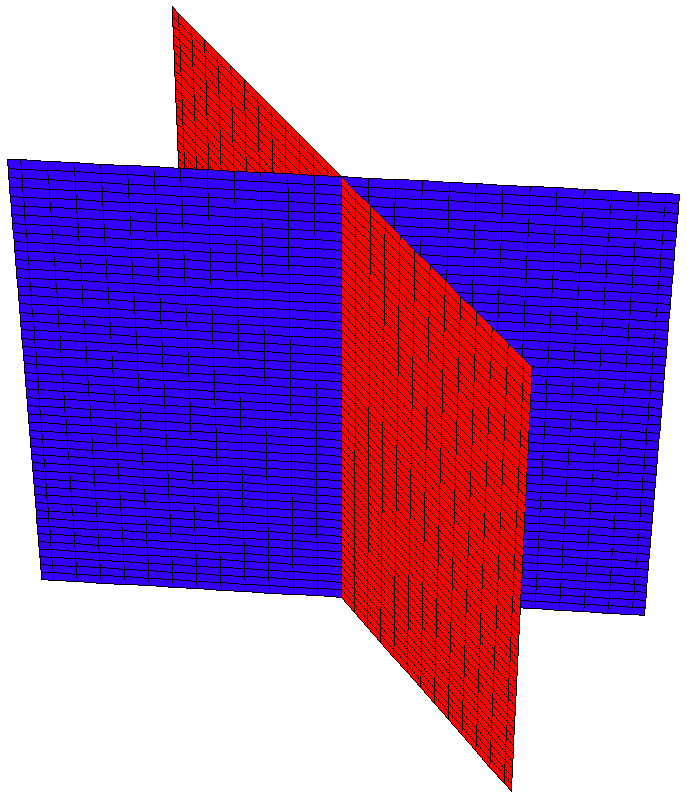
Mit der Normalform   $a\cdot x^2+b\cdot y^2=0$   mit   $a>0$, $b<0$   wird ein sich schneidendes Ebenenpaar beschrieben (Abbildung 2).

Diese Gleichung kann mittels Division umgeformt werden in eine Gleichung   $\frac{x^2}{p^2}-\frac{y^2}{q^2}=0$. Die beiden Ebenen schneiden die $x$-$y$-Ebene senkrecht in den Geraden $y=\mathrm{\pm }\frac{q}{p}\cdot x$.

Abbildung 2: Schnittebenenpaar mit der Flächengleichung   $4x^2-2y^2=0$